Vesiculation pathways in clathrin-mediated endocytosis

  1. Xinran Wang
  2. Julien Berro
  3. Rui Ma

  • Curated by eLife

    eLife logo

    eLife Assessment

    This valuable study proposes a theoretical model of clathrin coat formation based on membrane elasticity that seeks to determine whether this process occurs by increasing the area of a protein-coated patch with constant curvature, or by increasing the curvature of a protein-coated patch that forms in an initially flat conformation (so called constant curvature or constant area models). Identifying energetically favorable pathways and comparing the obtained shapes with experiments provides solid support to the constant-area pathway. This work will be of interest for biologists and biophysicists interested in membrane remodelling and endocytosis. It provides an innovative approach to tackle the question of constant curvature vs. constant area coat protein formation, although some of the model's assumption are only partially supported by experimental evidence.

Reviewed by

Read the full article See related articles

Discuss this preprint

Start a discussion What are Sciety discussions?

Listed in

Log in to save this article

Abstract

Abstract

During clathrin-mediated endocytosis, a patch of flat plasma membrane is internalized to form a vesicle. In mammalian cells, how the clathrin coat deforms the membrane into a vesicle remains unclear and two main hypotheses have been debated. The “constant area” hypothesis assumes that clathrin molecules initially form a flat lattice on the membrane and deform the membrane by changing its intrinsic curvature while keeping the coating area constant. The alternative “constant curvature” hypothesis assumes that the intrinsic curvature of the clathrin lattice remains constant during the formation of a vesicle while the surface area it covers increases. Previous experimental studies were unable to unambiguously determine which hypothesis is correct. In this paper, we show that these two hypotheses are only two extreme cases of a continuum of vesiculation pathways if we account for the free energies associated with clathrin assembly and curvature generation. By tracing the negative gradient of the free energy, we define vesiculation pathways in the phase space of the coating area and the intrinsic curvature of clathrin coat. Our results show that, overall, the differences in measurable membrane morphology between the different models are not as big as expected, and the main differences are most salient at the early stage of endocytosis. Furthermore, the best fitting pathway to experimental data is not compatible with the constant-curvature model and resembles a constant-area-like pathway where the coating area initially expands with minor changes in the intrinsic curvature, later followed by a dramatic increase in the intrinsic curvature and minor change in the coating area. Our results also suggest that experimental measurement of the tip radius and the projected area of the clathrin coat will be the key to distinguish between models.

Article activity feed

  1. eLife

    eLife Assessment

    This valuable study proposes a theoretical model of clathrin coat formation based on membrane elasticity that seeks to determine whether this process occurs by increasing the area of a protein-coated patch with constant curvature, or by increasing the curvature of a protein-coated patch that forms in an initially flat conformation (so called constant curvature or constant area models). Identifying energetically favorable pathways and comparing the obtained shapes with experiments provides solid support to the constant-area pathway. This work will be of interest for biologists and biophysicists interested in membrane remodelling and endocytosis. It provides an innovative approach to tackle the question of constant curvature vs. constant area coat protein formation, although some of the model's assumption are only partially supported by experimental evidence.

  2. eLife

    Reviewer #1 (Public review):

    Summary:

    The authors develop a set of biophysical models to investigate whether a constant area hypothesis or a constant curvature hypothesis explains the mechanics of membrane vesiculation during clathrin-mediated endocytosis.

    Strengths:

    The models that the authors choose are fairly well-described in the field and the manuscript is well-written.

    Weaknesses:

    One thing that is unclear is what is new with this work. If the main finding is that the differences are in the early stages of endocytosis, then one wonders if that should be tested experimentally. Also, the role of clathrin assembly and adhesion are treated as mechanical equilibrium but perhaps the process should not be described as equilibria but rather a time-dependent process. Ultimately, there are so many models that address this question that without direct experimental comparison, it's hard to place value on the model prediction.

    While an attempt is made to do so with prior published EM images, there is excessive uncertainty in both the data itself as is usually the case but also in the methods that are used to symmetrize the data. This reviewer wonders about any goodness of fit when such uncertainty is taken into account.

    Comments on revisions:

    I appreciate the authors edits, but I found that the major concerns I had still hold. Therefore, I did not alter my review.

  3. eLife

    Reviewer #2 (Public review):

    Summary:

    In this manuscript, the authors employ theoretical analysis of an elastic membrane model to explore membrane vesiculation pathways in clathrin-mediated endocytosis. A complete understanding of clathrin-mediated endocytosis requires detailed insight into the process of membrane remodeling, as the underlying mechanisms of membrane shape transformation remain controversial, particularly regarding membrane curvature generation. The authors compare constant area and constant membrane curvature as key scenarios by which clathrins induce membrane wrapping around the cargo to accomplish endocytosis. First, they characterize the geometrical aspects of the two scenarios and highlight their differences by imposing coating area and membrane spontaneous curvature. They then examine the energetics of the process to understand the driving mechanisms behind membrane shape transformations in each model. In the latter part, they introduce two energy terms: clathrin assembly or binding energy, and curvature generation energy, with two distinct approaches for the latter. Finally, they identify the energetically favorable pathway in the combined scenario and compare their results with experiments, showing that the constant-area pathway better fits the experimental data.

    Strengths:

    The manuscript is well-written, well-organized, and presents the details of the theoretical analysis with sufficient clarity.
    The calculations are valid, and the elastic membrane model is an appropriate choice for addressing the differences between the constant curvature and constant area models.
    The authors' approach of distinguishing two distinct free energy terms-clathrin assembly and curvature generation-and then combining them to identify the favorable pathway is both innovative and effective in addressing the problem.
    Notably, their identification of the energetically favorable pathways, and how these pathways either lead to full endocytosis or fail to proceed due to insufficient energetic drives, is particularly insightful.

    Comments on revisions:

    The authors have carefully addressed all my comments, and the revised manuscript is now clear, rigorous, and satisfactory.

  4. eLife

    Author response:

    The following is the authors’ response to the original reviews

    Reviewer #1:

    Summary

    The authors develop a set of biophysical models to investigate whether a constant area hypothesis or a constant curvature hypothesis explains the mechanics of membrane vesiculation during clathrin-mediated endocytosis.

    Strengths

    The models that the authors choose are fairly well-described in the field and the manuscript is wellwritten.

    Thank you for your positive comments on our work.

    Weaknesses

    One thing that is unclear is what is new with this work. If the main finding is that the differences are in the early stages of endocytosis, then one wonders if that should be tested experimentally. Also, the role of clathrin assembly and adhesion are treated as mechanical equilibrium but perhaps the process should not be described as equilibria but rather a time-dependent process. Ultimately, there are so many models that address this question that without direct experimental comparison, it's hard to place value on the model prediction.

    Thank you for your insightful questions. We fully agree that distinguishing between the two models should ultimately be guided by experimental tests. This is precisely the motivation for including Fig. 5 in our manuscript, where we compare our theoretical predictions with experimental data. In the middle panel of Fig. 5, we observe that the predicted tip radius as a function of 𝜓𝑚𝑎𝑥 from the constant curvature model (magenta curve) deviates significantly from both the experimental data points and the rolling median, highlighting the inconsistency of this model with the data.

    Regarding our treatment of clathrin assembly and membrane adhesion as mechanical equilibrium processes, our reasoning is based on a timescale separation argument. Clathrin assembly typically occurs over approximately 1 minute. In contrast, the characteristic relaxation time for a lipid membrane to reach mechanical equilibrium is given by 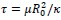, where 𝜇∼5 × 10-9 𝑁𝑠𝑚-1 is the membrane viscosity, 𝑅0 =50𝑛𝑚 is the vesicle size, 𝜅=20 𝑘𝐵𝑇 is the bending rigidity. This yields a relaxation time of 𝜏≈1.5 × 10−4𝑠, which is several orders of magnitude shorter than the timescale of clathrin assembly. Therefore, it is reasonable to treat the membrane shape as being in mechanical equilibrium throughout the assembly process.

    We believe the value of our model lies in the following key novelties:

    (1) Model novelty: We introduce an energy term associated with curvature generation, a contribution that is typically neglected in previous models.

    (2) Methodological novelty: We perform a quantitative comparison between theoretical predictions and experimental data, whereas most earlier studies rely on qualitative comparisons.

    (3) Results novelty: Our quantitative analysis enables us to unambiguously exclude the constant curvature hypothesis based on time-independent electron microscopy data.

    In the revised manuscript (line 141), we have added a statement about why we treat the clathrin assembly as in mechanical equilibrium.

    While an attempt is made to do so with prior published EM images, there is excessive uncertainty in both the data itself as is usually the case but also in the methods that are used to symmetrize the data. This reviewer wonders about any goodness of fit when such uncertainty is taken into account.

    Author response: We thank the reviewer for raising this important point. We agree that there is uncertainty in the experimental data. Our decision to symmetrize the data is based on the following considerations:

    (1) The experimental data provide a one-dimensional membrane profile corresponding to a cross-sectional view. To reconstruct the full two-dimensional membrane surface, we must assume rotational symmetry.

    (2)In addition to symmetrization, we also average membrane profiles within a certain range of 𝜓𝑚𝑎𝑥 values (see Fig. 5d). This averaging helps reduce the uncertainty (due to biological and experimental variability) inherent to individual measurements.

    (3)To further address the noise in the experimental data, we compare our theoretical predictions not only with individual data points but also with a rolling median, which provides a smoothed representation of the experimental trends.

    These steps are taken to ensure a more robust and meaningful comparison between theory and experiments.

    In the revised manuscript (line 338), we have explained why we have to symmetrize the data:

    “To facilitate comparison between the axisymmetric membrane shapes predicted by the model and the non-axisymmetric profiles obtained from electron microscopy, we apply a symmetrization procedure to the experimental data, which consist of one-dimensional membrane profiles extracted from cross-sectional views, as detailed in Appendix 3 (see also Appendix 3--Fig. 1).”

    Reviewer #2:

    Summary

    In this manuscript, the authors employ theoretical analysis of an elastic membrane model to explore membrane vesiculation pathways in clathrin-mediated endocytosis. A complete understanding of clathrin-mediated endocytosis requires detailed insight into the process of membrane remodeling, as the underlying mechanisms of membrane shape transformation remain controversial, particularly regarding membrane curvature generation. The authors compare constant area and constant membrane curvature as key scenarios by which clathrins induce membrane wrapping around the cargo to accomplish endocytosis. First, they characterize the geometrical aspects of the two scenarios and highlight their differences by imposing coating area and membrane spontaneous curvature. They then examine the energetics of the process to understand the driving mechanisms behind membrane shape transformations in each model. In the latter part, they introduce two energy terms: clathrin assembly or binding energy, and curvature generation energy, with two distinct approaches for the latter. Finally, they identify the energetically favorable pathway in the combined scenario and compare their results with experiments, showing that the constant-area pathway better fits the experimental data.

    Thank you for your clear and comprehensive summary of our work.

    Strengths

    The manuscript is well-written, well-organized, and presents the details of the theoretical analysis with sufficient clarity. The calculations are valid, and the elastic membrane model is an appropriate choice for addressing the differences between the constant curvature and constant area models.

    The authors' approach of distinguishing two distinct free energy terms-clathrin assembly and curvature generation-and then combining them to identify the favorable pathway is both innovative and effective in addressing the problem.

    Notably, their identification of the energetically favorable pathways, and how these pathways either lead to full endocytosis or fail to proceed due to insufficient energetic drives, is particularly insightful.

    Thank you for your positive remarks regarding the innovative aspects of our work.

    Weaknesses and Recommendations

    Weakness: Membrane remodeling in cellular processes is typically studied in either a constant area or constant tension ensemble. While total membrane area is preserved in the constant area ensemble, membrane area varies in the constant tension ensemble. In this manuscript, the authors use the constant tension ensemble with a fixed membrane tension, σe. However, they also use a constant area scenario, where 'area' refers to the surface area of the clathrin-coated membrane segment. This distinction between the constant membrane area ensemble and the constant area of the coated membrane segment may cause confusion.

    Recommendation: I suggest the authors clarify this by clearly distinguishing between the two concepts by discussing the constant tension ensemble employed in their theoretical analysis.

    Thank you for raising this question.

    In the revised manuscript (line 136), we have added a sentence, emphasizing the implication of the term “constant area model”:

    “We emphasize that the constant area model refers to the assumption that the clathrin-coated area 𝑎0 remains fixed. Meanwhile, the membrane tension 𝜎𝑒 at the base is held constant, allowing the total membrane area 𝐴𝐴 to vary in response to deformations induced by the clathrin coat.”

    Weakness: As mentioned earlier, the theoretical analysis is performed in the constant membrane tension ensemble at a fixed membrane tension. The total free energy E_tot of the system consists of membrane bending energy E_b and tensile energy E_t, which depends on membrane tension, σe. Although the authors mention the importance of both E_b and E_t, they do not present their individual contributions to the total energy changes. Comparing these contributions would enable readers to cross-check the results with existing literature, which primarily focuses on the role of membrane bending rigidity and membrane tension.

    Recommendation: While a detailed discussion of how membrane tension affects their results may fall outside the scope of this manuscript, I suggest the authors at least discuss the total membrane area variation and the contribution of tensile energy E_t for the singular value of membrane tension used in their analysis.

    Thank you for the insightful suggestion. In the revised manuscript (line 916), we have added Appendix 6 and a supplementary figure to compare the bending energy 𝐸𝑏 and the tension energy 𝐸𝑡. Our analysis shows that both energy components exhibit an energy barrier between the flat and vesiculated membrane states, with the tension energy contributing more significantly than the bending energy.

    In the revised manuscript (line 151), we have also added one paragraph explaining why we set the dimensionless tension 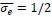. This choice is motivated by our use of the characteristic length 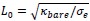as the length scale, and 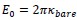as the energy scale. In this way, the dimensionless tension energy is written as

    Where 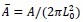is the dimensionless area.

    Weakness: The authors introduce two different models, (1,1) and (1,2), for generating membrane curvature. Model 1 assumes a constant curvature growth, corresponding to linear curvature growth, while Model 2 relates curvature growth to its current value, resembling exponential curvature growth. Although both models make physical sense in general, I am concerned that Model 2 may lead to artificial membrane bending at high curvatures. Normally, for intermediate bending, ψ > 90, the bending process is energetically downhill and thus proceeds rapidly. The bending process is energetically downhill and thus proceeds rapidly. However, Model 2's assumption would accelerate curvature growth even further. This is reflected in the endocytic pathways represented by the green curves in the two rightmost panels of Fig. 4a, where the energy steeply increases at large ψ. I believe a more realistic version of Model 2 would require a saturation mechanism to limit curvature growth at high curvatures.

    Recommendation 1: I suggest the authors discuss this point and highlight the pros and cons of Model 2. Specifically, addressing the potential issue of artificial membrane bending at high curvatures and considering the need for a saturation mechanism to limit excessive curvature growth. A discussion on how Model 2 compares to Model 1 in terms of physical relevance, especially in the context of high curvature scenarios, would provide valuable insights for the reader.

    Thank you for raising the question of excessive curvature growth in our models and the constructive suggestion of introducing a saturation mechanism. In the revised manuscript (line 405), following your recommendation, we have added a subsection “Saturation effect at high membrane curvatures” in the discussion to clarify the excessive curvature issue and a possible way to introduce a saturation mechanism:

    “Note that our model involves two distinct concepts of curvature growth. The first is the growth of imposed curvature — referred to here as intrinsic curvature and denoted by the parameter 𝑐0 — which is driven by the reorganization of bonds between clathrin molecules within the coat. The second is the growth of the actual membrane curvature, reflected by the increasing value of 𝜓𝑚𝑎𝑥.

    The latter process is driven by the former.

    Models (1,1) and (1,2) incorporate energy terms (Equation 6) that promote the increase of intrinsic curvature 𝑐0, which in turn drives the membrane to adopt a more curved shape (increasing 𝜓𝑚𝑎𝑥). In the absence of these energy contributions, the system faces an energy barrier separating a weakly curved membrane state (low 𝜓𝑚𝑎𝑥) from a highly curved state (high 𝜓𝑚𝑎𝑥). This barrier can be observed, for example, in the red curves of Figure 3(a–c) and in Appendix 6—Figure 1. As a result, membrane bending cannot proceed spontaneously and requires additional energy input from clathrin assembly.

    The energy terms described in Equation 6 serve to eliminate this energy barrier by lowering the energy difference between the uphill and downhill regions of the energy landscape. However, these same terms also steepen the downhill slope, which may lead to overly aggressive curvature growth.

    To mitigate this effect, one could introduce a saturation-like energy term of the form:

    where 𝑐𝑠 represents a saturation curvature. Importantly, adding such a term would not alter the conclusions of our study, since the energy landscape already favors high membrane curvature (i.e., it is downward sloping) even without the additional energy terms. “

    Recommendation 2: Referring to the previous point, the green curves in the two rightmost panels of Fig. 4a seem to reflect a comparison between slow and fast bending regimes. The initial slow vesiculation (with small curvature growth) in the left half of the green curves is followed by much more rapid curvature growth beyond a certain threshold. A similar behavior is observed in Model 1, as shown by the green curves in the two rightmost panels of Fig. 4b. I believe this transition between slow and fast bending warrants a brief discussion in the manuscript, as it could provide further insight into the dynamic nature of vesiculation.

    Thank you for your constructive suggestion regarding the transition between slow and fast membrane bending. As you pointed out, in both Fig. 4a (model (1,2)) and Fig. 4b (model (1,1)), the green curves tend to extend vertically at the late stage. This suggests a significant increase in 𝑐0 on the free energy landscape. However, we remain cautious about directly interpreting this vertical trend as indicative of fast endocytic dynamics, since our model is purely energetic and does not explicitly incorporate kinetic details. Meanwhile, we agree with your observation that the steep decrease in free energy along the green curve could correspond to an acceleration in dynamics. To address this point, we have added a paragraph in the revised manuscript (in Subsection “Cooperativity in the curvature generation process”) discussing this potential transition and its consistency with experimental observations (line 395):

    “Furthermore, although our model is purely energetic and does not explicitly incorporate dynamics, we observe in Figure 3(a) that along the green curve—representing the trajectory predicted by model (1,2)—the total free energy (𝐸𝑡𝑜𝑡) exhibits a much sharper decrease at the late stage (near the vesiculation line) compared to the early stage (near the origin). This suggests a transition from slow to fast dynamics during endocytosis. Such a transition is consistent with experimental observations, where significantly fewer number of images with large 𝜓𝑚𝑎𝑥 are captured compared to those with small 𝜓𝑚𝑎𝑥 (Mund et al., 2023).”

    The geometrical properties of both the constant-area and constant-curvature scenarios, as well depicted in Fig. 1, are somewhat straightforward. I wonder what additional value is presented in Fig. 2. Specifically, the authors solve differential shape equations to show how Rt and Rcoat vary with the angle ψ, but this behavior seems predictable from the simple schematics in Fig. 1. Using a more complex model for an intuitively understandable process may introduce counter-intuitive results and unnecessary complications, as seen with the constant-curvature model where Rt varies (the tip radius is not constant, as noted in the text) despite being assumed constant. One could easily assume a constant-curvature model and plot Rt versus ψ. I wonder What is the added value of solving shape equations to measure geometrical properties, compared to a simpler schematic approach (without solving shape equations) similar to what they do in App. 5 for the ratio of the Rt at ψ=30 and 150.

    Thank you for raising this important question. While simple and intuitive theoretical models are indeed convenient to use, their validity must be carefully assessed. The approximate model becomes inaccurate when the clathrin shell significantly deviates from its intrinsic shape, namely a spherical cap characterized by intrinsic curvature 𝑐0. As shown in the insets of Fig. 2b and 2c (red line and black points), our comparison between the simplified model and the full model demonstrates that the simple model provides a good approximation under the constant-area constraint. However, it performs poorly under the constant-curvature constraint, and the deviation between the full model and the simplified model becomes more pronounced as 𝑐0 increases.

    In the revised manuscript, we have added a sentence emphasizing the discrepancy between the exact calculation with the idealized picture for the constant curvature model (line 181):

    “For the constant-curvature model, the ratio remains close to 1 only at small values of 𝑐0, as expected from the schematic representation of the model in Figure 1. However, as 𝑐0 increases, the deviation from this idealized picture becomes increasingly pronounced.”

    Recommendation: The clathrin-mediated endocytosis aims at wrapping cellular cargos such as viruses which are typically spherical objects which perfectly match the constant-curvature scenario. In this context, wrapping nanoparticles by vesicles resembles constant-curvature membrane bending in endocytosis. In particular analogous shape transitions and energy barriers have been reported (similar to Fig.3 of the manuscript) using similar theoretical frameworks by varying membrane particle binding energy acting against membrane bending:

    DOI: 10.1021/la063522m

    DOI: 10.1039/C5SM01793A

    I think a short comparison to particle wrapping by vesicles is warranted.

    Thank you for your constructive suggestion to compare our model with particle wrapping. In the revised manuscript (line 475), we have added a subsection “Comparison with particle wrapping” in the discussion:

    “The purpose of the clathrin-mediated endocytosis studied in our work is the recycling of membrane and membrane-protein, and the cellular uptake of small molecules from the environment — molecules that are sufficiently small to bind to the membrane or be encapsulated within a vesicle. In contrast, the uptake of larger particles typically involves membrane wrapping driven by adhesion between the membrane and the particle, a process that has also been studied previously (Góźdź, 2007; Bahrami et al., 2016). In our model, membrane bending is driven by clathrin assembly, which induces curvature. In particle wrapping, by comparison, the driving force is the adhesion between the membrane and a rigid particle. In the absence of adhesion, wrapping increases both bending and tension energies, creating an energy barrier that separates the flat membrane state from the fully wrapped state. This barrier can hinder complete wrapping, resulting in partial or no engulfment of the particle. Only when the adhesion energy is sufficiently strong can the process proceed to full wrapping. In this context, adhesion plays a role analogous to curvature generation in our model, as both serve to overcome the energy barrier. If the particle is spherical, it imposes a constant-curvature pathway during wrapping. However, the role of clathrin molecules in this process remains unclear and will be the subject of future investigation.”

    Minor points:

    Line 20, abstract, "....a continuum spectrum ..." reads better.

    Line 46 "...clathrin results in the formation of pentagons ...." seems Ito be grammatically correct.

    Line 106, proper citation of the relevant literature is warranted here.

    Line 111, the authors compare features (plural) between experiments and calculations. I would write "....compare geometric features calculated by theory with those ....".

    Line 124, "Here, we choose a ..." (with comma after Here).

    Line 134, "The membrane tension \sigma_e and bending rigidity \kappa define a ...."

    Line 295, "....tip radius, and invagination ...." (with comma before and).

    Line 337, "abortive tips, and ..." (with comma before and).

    We thank you for your thorough review of our manuscript and have corrected all the issues raised.

  5. eLife

    eLife Assessment

    This valuable study proposes a theoretical model of clathrin coat formation based on membrane elasticity that seeks to determine whether this process occurs by increasing the area of a protein-coated patch with constant curvature, or by increasing the curvature of a protein-coated patch that forms in an initially flat conformation (so called constant curvature or constant area models). Identifying energetically favorable pathways and comparing the obtained shapes with experiments provides solid support to the constant-area pathway. This work will be of interest for biologists and biophysicists interested in membrane remodelling and endocytosis. It provides an innovative approach to tackle the question of constant curvature vs. constant area coat protein formation, although some of the model's assumption are only partially supported by experimental evidence.

  6. eLife

    Reviewer #1 (Public review):

    Summary:

    The authors develop a set of biophysical models to investigate whether a constant area hypothesis or a constant curvature hypothesis explains the mechanics of membrane vesiculation during clathrin-mediated endocytosis.

    Strengths:

    The models that the authors choose are fairly well-described in the field and the manuscript is well-written.

    Weaknesses:

    One thing that is unclear is what is new with this work. If the main finding is that the differences are in the early stages of endocytosis, then one wonders if that should be tested experimentally. Also, the role of clathrin assembly and adhesion are treated as mechanical equilibrium but perhaps the process should not be described as equilibria but rather a time-dependent process. Ultimately, there are so many models that address this question that without direct experimental comparison, it's hard to place value on the model prediction.
    While an attempt is made to do so with prior published EM images, there is excessive uncertainty in both the data itself as is usually the case but also in the methods that are used to symmetrize the data. This reviewer wonders about any goodness of fit when such uncertainty is taken into account.

  7. eLife

    Reviewer #2 (Public review):

    Summary:

    In this manuscript, the authors employ theoretical analysis of an elastic membrane model to explore membrane vesiculation pathways in clathrin-mediated endocytosis. A complete understanding of clathrin-mediated endocytosis requires detailed insight into the process of membrane remodeling, as the underlying mechanisms of membrane shape transformation remain controversial, particularly regarding membrane curvature generation. The authors compare constant area and constant membrane curvature as key scenarios by which clathrins induce membrane wrapping around the cargo to accomplish endocytosis. First, they characterize the geometrical aspects of the two scenarios and highlight their differences by imposing coating area and membrane spontaneous curvature. They then examine the energetics of the process to understand the driving mechanisms behind membrane shape transformations in each model. In the latter part, they introduce two energy terms: clathrin assembly or binding energy, and curvature generation energy, with two distinct approaches for the latter. Finally, they identify the energetically favorable pathway in the combined scenario and compare their results with experiments, showing that the constant-area pathway better fits the experimental data.

    Strengths:

    The manuscript is well-written, well-organized, and presents the details of the theoretical analysis with sufficient clarity.
    The calculations are valid, and the elastic membrane model is an appropriate choice for addressing the differences between the constant curvature and constant area models.
    The authors' approach of distinguishing two distinct free energy terms-clathrin assembly and curvature generation-and then combining them to identify the favorable pathway is both innovative and effective in addressing the problem.
    Notably, their identification of the energetically favorable pathways, and how these pathways either lead to full endocytosis or fail to proceed due to insufficient energetic drives, is particularly insightful.

    Weaknesses:

    Membrane remodeling in cellular processes is typically studied in either a constant area or constant tension ensemble. While total membrane area is preserved in the constant area ensemble, membrane area varies in the constant tension ensemble. In this manuscript, the authors use the constant tension ensemble with a fixed membrane tension, σe. However, they also use a constant area scenario, where 'area' refers to the surface area of the clathrin-coated membrane segment. This distinction between the constant membrane area ensemble and the constant area of the coated membrane segment may cause confusion.

    As mentioned earlier, the theoretical analysis is performed in the constant membrane tension ensemble at a fixed membrane tension. The total free energy E_tot of the system consists of membrane bending energy E_b and tensile energy E_t, which depends on membrane tension, σe. Although the authors mention the importance of both E_b and E_t, they do not present their individual contributions to the total energy changes. Comparing these contributions would enable readers to cross-check the results with existing literature, which primarily focuses on the role of membrane bending rigidity and membrane tension.

    The authors introduce two different models, (1,1) and (1,2), for generating membrane curvature. Model 1 assumes a constant curvature growth, corresponding to linear curvature growth, while Model 2 relates curvature growth to its current value, resembling exponential curvature growth. Although both models make physical sense in general, I am concerned that Model 2 may lead to artificial membrane bending at high curvatures. Normally, for intermediate bending, ψ > 90, the bending process is energetically downhill and thus proceeds rapidly. the bending process is energetically downhill and thus proceeds rapidly. However, Model 2's assumption would accelerate curvature growth even further. This is reflected in the endocytic pathways represented by the green curves in the two rightmost panels of Fig. 4a, where the energy steeply increases at large ψ. I believe a more realistic version of Model 2 would require a saturation mechanism to limit curvature growth at high curvatures.

  8. Version published to 10.7554/elife.102591.1 on eLife
  9. Version published to 10.7554/elife.102591 on eLife
  10. Version published to 10.1101/2024.08.13.607731 on bioRxiv