How to assemble a scale-invariant gradient
Curation statements for this article:-
Curated by eLife
Evaluation Summary:
How biological patterns such as concentration gradient scale with the size of the cell or organism is a long-standing question in developmental and cell biology. In this study, Datta et al show theoretically that directed membrane transport of biomolecules and their release at the cell pole results in a cytoplasmic gradient that scales with cell size if two requirements are met: the cell grows while maintaining its spheroid proportions, (i.e. not by elongation), and the binding of the cytoplasmic fraction of the biomolecule to the membrane should be close to irreversible. A strength of this manuscript is that it invokes a realistic cellular mechanism that could be achieved through several biochemical implementations and can inspire experimental studies. Stronger biological examples and a deeper search in the literature or change in some of the simulation parameters would improve the study, and give the "impetus for experiments" the authors wish to provide.
(This preprint has been reviewed by eLife. We include the public reviews from the reviewers here; the authors also receive private feedback with suggested changes to the manuscript. The reviewers remained anonymous to the authors.)
This article has been Reviewed by the following groups
Discuss this preprint
Start a discussion What are Sciety discussions?Listed in
- Evaluated articles (eLife)
Abstract
Intracellular protein gradients serve a variety of functions, such as the establishment of cell polarity or to provide positional information for gene expression in developing embryos. Given that cell size in a population can vary considerably, for the protein gradients to work properly they often have to be scaled to the size of the cell. Here, we examine a model of protein gradient formation within a cell that relies on cytoplasmic diffusion and cortical transport of proteins toward a cell pole. We show that the shape of the protein gradient is determined solely by the cell geometry. Furthermore, we show that the length scale over which the protein concentration in the gradient varies is determined by the linear dimensions of the cell, independent of the diffusion constant or the transport speed. This gradient provides scale-invariant positional information within a cell, which can be used for assembly of intracellular structures whose size is scaled to the linear dimensions of the cell, such as the cytokinetic ring and actin cables in budding yeast cells.
Article activity feed
-

-

Author Respoinse
Reviewer #2 (Public Review):
In the results of Fig. 2, the proteins are emitted at distance epsilon from the cortical boundary. From there, they locally perform 1D diffusion to the boundary, so most of them would readsorb once they diffuse a distance epsilon. Only a small fraction would extend past epsilon, which I assume is why the concentration drops by orders of magnitude beyond epsilon. Is such a concentration drop realistic given typical numbers of proteins in cells?
This is a good point. In [29], McInally et al. investigate kinesin-13 concentrations in Giardia and find that it drops sharply near the pole (about three to four orders of magnitude), as surmised by the referee. The drop off we see in our model is like what McInally et al see in terms of orders of magnitude decrease in the concentration gradient …
Author Respoinse
Reviewer #2 (Public Review):
In the results of Fig. 2, the proteins are emitted at distance epsilon from the cortical boundary. From there, they locally perform 1D diffusion to the boundary, so most of them would readsorb once they diffuse a distance epsilon. Only a small fraction would extend past epsilon, which I assume is why the concentration drops by orders of magnitude beyond epsilon. Is such a concentration drop realistic given typical numbers of proteins in cells?
This is a good point. In [29], McInally et al. investigate kinesin-13 concentrations in Giardia and find that it drops sharply near the pole (about three to four orders of magnitude), as surmised by the referee. The drop off we see in our model is like what McInally et al see in terms of orders of magnitude decrease in the concentration gradient close to the pole.
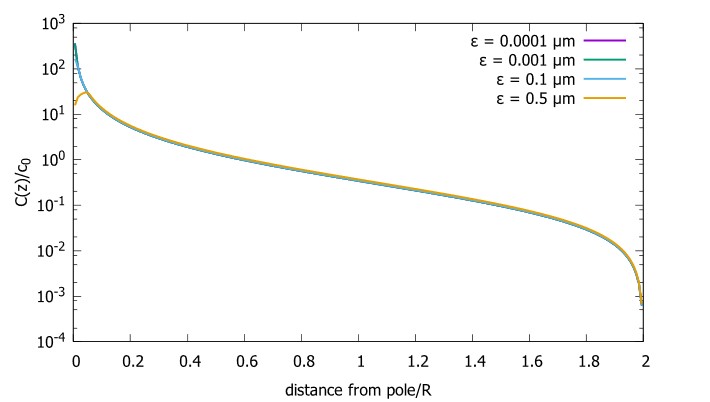
It should be clarified if the proposed size scaling is independent of the specific choice of the distance epsilon of the point of protein release from the anterior pole. I don't see any reason why this distance should increase with cell size as epsilon = 0.05 R (on page with equation 5). It's unclear if the size scaling of the concentration gradient might be dependent on the assumption epsilon ~ R.
Figure R1 shows the dependence of the gradient on epsilon and see that the concentration gradient from the pole is unaffected everywhere beyond the source.
Figure R1. Concentration gradient for cells with the source at different distances from the pole (ϵ) Concentration profiles with differing source points. We start very close to the pole and move further away. The radius of the sphere is 10 μm, the diffusion constant D=1 μm^2/s and the transport speed along the cortex is v=1μm/s.
-

Evaluation Summary:
How biological patterns such as concentration gradient scale with the size of the cell or organism is a long-standing question in developmental and cell biology. In this study, Datta et al show theoretically that directed membrane transport of biomolecules and their release at the cell pole results in a cytoplasmic gradient that scales with cell size if two requirements are met: the cell grows while maintaining its spheroid proportions, (i.e. not by elongation), and the binding of the cytoplasmic fraction of the biomolecule to the membrane should be close to irreversible. A strength of this manuscript is that it invokes a realistic cellular mechanism that could be achieved through several biochemical implementations and can inspire experimental studies. Stronger biological examples and a deeper search in the …
Evaluation Summary:
How biological patterns such as concentration gradient scale with the size of the cell or organism is a long-standing question in developmental and cell biology. In this study, Datta et al show theoretically that directed membrane transport of biomolecules and their release at the cell pole results in a cytoplasmic gradient that scales with cell size if two requirements are met: the cell grows while maintaining its spheroid proportions, (i.e. not by elongation), and the binding of the cytoplasmic fraction of the biomolecule to the membrane should be close to irreversible. A strength of this manuscript is that it invokes a realistic cellular mechanism that could be achieved through several biochemical implementations and can inspire experimental studies. Stronger biological examples and a deeper search in the literature or change in some of the simulation parameters would improve the study, and give the "impetus for experiments" the authors wish to provide.
(This preprint has been reviewed by eLife. We include the public reviews from the reviewers here; the authors also receive private feedback with suggested changes to the manuscript. The reviewers remained anonymous to the authors.)
-

Reviewer #1 (Public Review):
How biological pattern scales with the size of the cell or organism is a long-standing question in developmental and cell biology. While there are many mechanisms to form a gradient, only a few convey scaling of the gradient with size. In this study, Datta et al present a theoretical study that analyzes the formation of an intracellular cytoplasmatic gradient as a result of membrane transport of the biomolecules and their release in a pole of the cell.
The authors provide two main requirements for the cytoplasmatic gradient to scale with cell size:
1. The cell geometry should be close to spherical or more generally grow while maintaining its spheroid proportions, and not grow via elongation.
2. The binding of the cytoplasmatic fraction of the biomolecule to the membrane (e.g. to motor proteins) should be …Reviewer #1 (Public Review):
How biological pattern scales with the size of the cell or organism is a long-standing question in developmental and cell biology. While there are many mechanisms to form a gradient, only a few convey scaling of the gradient with size. In this study, Datta et al present a theoretical study that analyzes the formation of an intracellular cytoplasmatic gradient as a result of membrane transport of the biomolecules and their release in a pole of the cell.
The authors provide two main requirements for the cytoplasmatic gradient to scale with cell size:
1. The cell geometry should be close to spherical or more generally grow while maintaining its spheroid proportions, and not grow via elongation.
2. The binding of the cytoplasmatic fraction of the biomolecule to the membrane (e.g. to motor proteins) should be close to irreversible.A strength of this manuscript is that it invokes a cellular mechanism that is imaginable and could be achieved through several biochemical implementations and can inspire experimental studies. The analytical arguments and the figures can be understood by biologists that value theory while the analogies to electrostatics and analytical solutions are informative for readers with a physics background.
A weakness of this paper is that the biological examples the authors provide are not convincing. A deeper search in the literature or change in some of the simulation parameters can improve the study, and give the "impetus for experiments" the authors wish to provide.
For example, the size range of yeast is an order of magnitude smaller than simulated. In Giardia, a system that the authors are well familiar with, the gradient does not scale with size. This is in accordance with the theory, but to show the theory's applicability, data on how the gradient scales with the radius of the flagella is required and not a general agreement. Achieving a gradient that doesn't scale is much easier and does not require the theory. The Bicoid system, which has been studied extensively, also does not appear to be a good example for the implementation of this mechanism. The c. elegans embryo system cited also does not appear to fit the model. There is very good data on the gradient formation in most of the systems described, which can be used to test the predictions of this model on scaling.
Altogether, the theoretical grounds of the model presented by Datta et al are sound, and the results are interesting and valuable to the developmental/cell bio community. To make this study better, the authors would need to show greater relevance to existing data.
-

Reviewer #2 (Public Review):
The authors propose a novel concentration scaling mechanism through transport and diffusion. While this is somewhat surprising, given extensive past work on transport-diffusion systems, I have not encountered the arguments presented by the authors in prior work myself.
For the polar transport case considered in Figure 2, the problem that is solved is essentially that of the concentration gradient resulting from a point source near an absorbing boundary (the boundary is perfectly absorbing and all captured proteins are transported to the anterior pole). Indeed, the resulting concentration profile would only depend on the geometry of random walks starting from the anterior pole and reaching the absorbing boundary. Thus, in this limit, it's a straightforward result that the concentration gradient does not …
Reviewer #2 (Public Review):
The authors propose a novel concentration scaling mechanism through transport and diffusion. While this is somewhat surprising, given extensive past work on transport-diffusion systems, I have not encountered the arguments presented by the authors in prior work myself.
For the polar transport case considered in Figure 2, the problem that is solved is essentially that of the concentration gradient resulting from a point source near an absorbing boundary (the boundary is perfectly absorbing and all captured proteins are transported to the anterior pole). Indeed, the resulting concentration profile would only depend on the geometry of random walks starting from the anterior pole and reaching the absorbing boundary. Thus, in this limit, it's a straightforward result that the concentration gradient does not depend on diffusion coefficient or transport speed, as stated in the abstract.
However, I have two main concerns regarding the proposed mechanism. The first is regarding the steepness of the concentration gradient. In the results of Fig. 2, the proteins are emitted at distance epsilon from the cortical boundary. From there, they locally perform 1D diffusion to the boundary, so most of them would readsorb once they diffuse a distance epslilon. Only a small fraction would extend past epsilon, which I assume is why the concentration drops by orders of magnitude beyond epsilon. Is such a concentration drop realistic given typical numbers of proteins in cells?
Secondly, it should be clarified if the proposed size scaling is independent of the specific choice of the distance epsilon of the point of protein release from the anterior pole. I don't see any reason why this distance should increase with cell size as epsilon = 0.05 R (on page with equation 5). It's unclear if the size scaling of the concentration gradient might be dependent on the assumption epsilon ~ R (though after plotting the expressions presented in equations 5 and 6, it seems to me that the scaling is independent of epsilon at distances larger than epsilon).
Finally, what seems to me to be the most important is to provide better quantitative biological examples of systems likely to exploit such mechanisms. A lot is known already quantitatively about several model organisms/cell systems. The absence of quantitative comparisons is suggesting that perhaps the proposed mechanism might not withstand further scrutiny. For example, how might this mechanism control the scaling of the budding yeast septin ring mentioned in the introduction? What would be the corresponding kon rate given the known density of actin cables? And can one use the knowledge from this work to check if the systems mentioned in the introduction (such as MEX-5, Pom1) might realize or not the proposed mechanism?
-