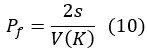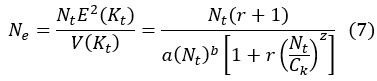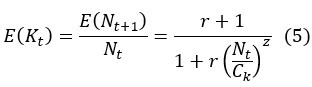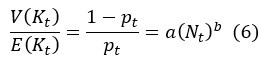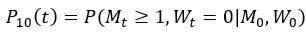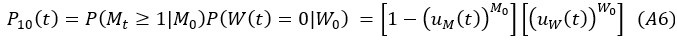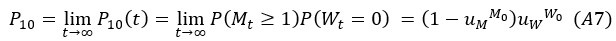The Generalized Haldane (GH) model tracking population size changes and resolving paradoxes of genetic drift
Curation statements for this article:-
Curated by eLife
eLife Assessment
This study presents a useful model of genetic drift by incorporating variance in reproductive success, aiming to address several apparent paradoxes in molecular evolution. However, some of the apparent paradoxes only arise in the most basic version of standard models and have been reconciled in more advanced models. Nonetheless, this paper offers intuitive explanations for these apparent paradoxes, by adopting a new perspective and solid modeling and analysis. More broadly, the proposed model provides an alternative framework to address puzzling observations in molecular evolution, which will be of interest to evolutionary and population geneticists.
This article has been Reviewed by the following groups
Discuss this preprint
Start a discussion What are Sciety discussions?Listed in
- Evaluated articles (eLife)
Abstract
Abstract
Population genetic models, such as the Wright-Fisher (WF) model, track relative gene frequencies. The absolute gene copy number, or population size (N), is supplied externally for tracking genetic drift. JBS Haldane (1927) proposed an alternative model based on the branching process, whereby each gene copy is transmitted to K descendants with the mean and variance of E(K) and V(K). In this model, E(K) governs N, while V(K)/N governs genetic drift. Nevertheless, as the branching process allows N to drift unboundedly, a Generalized Haldane (GH) model that regulates N more tightly is proposed. The GH model can account for several paradoxes of molecular evolution. Notably, genetic drift may often become stronger as N becomes larger in the ecological setting, thus contradicting the general view. In particular, a very small population growing exponentially experiences little drift. Interestingly, when the population grows and N oscillates near the carrying capacity, the paradoxical trend is also observed in both field works and laboratory experiments. This paradox whereby population size in genetics (Ne) and ecology (N) could be negatively correlated is resolved by the GH model. Additional paradoxes include ii) The two sexes experiencing drift differently; iii) Genetic drift of advantageous mutations being independent of N; iv) Multi-copy gene systems (viruses, mitochondria, etc.) having no definable Ne (for effective N). In brief, the GH model defines genetic drift simply as V(K), or V(K)/N averaged over the population. It represents an attempt at integrating genetical and ecological analyses into one framework.
Article activity feed
-

eLife Assessment
This study presents a useful model of genetic drift by incorporating variance in reproductive success, aiming to address several apparent paradoxes in molecular evolution. However, some of the apparent paradoxes only arise in the most basic version of standard models and have been reconciled in more advanced models. Nonetheless, this paper offers intuitive explanations for these apparent paradoxes, by adopting a new perspective and solid modeling and analysis. More broadly, the proposed model provides an alternative framework to address puzzling observations in molecular evolution, which will be of interest to evolutionary and population geneticists.
-

Reviewer #1 (Public review):
The revision by Ruan et al clarifies several aspects of the original manuscript that were difficult to understand, and I think it presents some useful and interesting ideas. I understand that the authors are distinguishing their model from the standard Wright-Fisher model in that the population size is not imposed externally, but is instead a consequence of the stochastic reproduction scheme. Here, the authors chose a branching process but in principle any Markov chain can probably be used. Within this framework, the authors are particularly interested in cases where the variance in reproductive success changes through time, as explored by the DDH model, for example. They argue with some experimental results that there is a reason to believe that the variance in reproductive success does change over time.
One…
Reviewer #1 (Public review):
The revision by Ruan et al clarifies several aspects of the original manuscript that were difficult to understand, and I think it presents some useful and interesting ideas. I understand that the authors are distinguishing their model from the standard Wright-Fisher model in that the population size is not imposed externally, but is instead a consequence of the stochastic reproduction scheme. Here, the authors chose a branching process but in principle any Markov chain can probably be used. Within this framework, the authors are particularly interested in cases where the variance in reproductive success changes through time, as explored by the DDH model, for example. They argue with some experimental results that there is a reason to believe that the variance in reproductive success does change over time.
One of the key aspects of the original manuscript that I want to engage with is the DDH model. As the authors point out, their equations 5 and 6 are assumptions, and not derived from any principles. In essence, the authors are positing that that the variance in reproductive success, given by 6, changes as a function of the current population size. There is nothing "inherent" to a negative binomial branching mechanism that results in this: in fact, the the variance in offspring number could in principle be the same for all time. As relates to models that exist in the literature, I believe that this is the key difference: unlike Cannings models, the authors allow for a changing variance in reproduction through time.
This is, of course, an interesting thing to consider, and I think that the situation the authors point out, in which drift is lower at small population sizes and larger at large population sizes, is not appreciated in the literature. However, I am not so sure that there is anything that needs to be resolved in Paradox 1. A very strong prediction of that model is that Ne and N could be inversely related, as shown by the blue line in Fig 3b. This suggests that you could see something very strange if you, for example, infer a population size history using a Wright-Fisher framework, because you would infer a population *decline* when there is in fact a population *expansion*. However, as far as I know there are very few "surprising population declines" found in empirical data. An obvious case where we know there is very rapid population growth is human populations; I don't think I've ever seen an inference of recent human demographic history from genetic data that suggests anything other than a massive population expansion. While I appreciate the authors empirical data supporting their claim of Paradox 1 (more on the empirical data later), it's not clear to me that there's a "paradox" in the literature that needs explaining so much as this is a "words of caution about interpreting inferred effective population sizes". To be clear, I think those words of caution are important, and I had never considered that you might be so fundamentally misled as to infer decline when there is growth, but calling it a "paradox" seems to suggest that this is an outstanding problem in the literature, when in fact I think the authors are raising a *new* and important problem. Perhaps an interesting thing for the authors to do to raise the salience of this point would be to perform simulations under this model and then infer effective population sizes using e.g. dadi or psmc and show that you could identify a situation in which the true history is one of growth, but the best fit would be one of decline
The authors also highlight that their approach reflects a case where the population size is determined by the population dynamics themselves, as opposed to being imposed externally as is typical in Cannings models. I agree with the authors that this aspect of population regulation is understudied. Nonetheless, several manuscripts have dealt with the case of population genetic dynamics in populations of stochastically fluctuating size. For example, Kaj and Krone (2003) show that under pretty general conditions you get something very much like a standard coalescent; for example, combining their theorem 1 with their arguments on page 36 and 37, they find that exchangeable populations with stochastic population dynamics where the variance does not change with time still converge to exactly the coalescent you would expect from Cannings models. This is strongly suggestive that the authors key result isn't about stochastic population dynamics per se, but instead related to arguing that variance in reproductive success could change through time. In fact, I believe that the result of Kaj and Krone (2003) is substantially more general than the models considered in this manuscript. That being said, I believe that the authors of this manuscript do a much better job of making the implications for evolutionary processes clear than Kaj and Krone, which is important---it's very difficult to understand from Kaj and Krone the conditions under which effective population sizes will be substantially impacted by stochastic population dynamics.
I also find the authors exposition on Paradox 3 to be somewhat strange. First of all, I'm not sure there's a paradox there at all? The authors claim that the lack of dependence of the fixation probability on Ne is a paradox, but this is ultimately not surprising---fixation of a positively selected allele depends mostly on escaping the boundary layer, which doesn't really depend on the population size (see Gillespie's book "The Causes of Molecular Evolution" for great exposition on boundary layer effects). Moreover, the authors *use a Cannings-style argument* to get gain a good approximation of how the fixation probability changes when there is non-Poisson reproduction. So it's not clear that the WFH model is really doing a lot of work here. I suppose they raise the interesting point that the particularly simple form of p(fix) = 2s is due to the assumption that variance in offspring is equal to 1.
In addition, I raised some concerns about the analysis of empirical results on reproductive variance in my original review, and I don't believe that the authors responded to it at all. I'm not super worried about that analysis, but I think that the authors should probably respond to me.
Overall, I feel like I now have a better understanding of this manuscript. However, I think it still presents its results too strongly: Paradox 1 contains important words of caution that reflect what I am confident is an under appreciated possibility, and Paradox 3 is, as far as I'm concerned, not a paradox at all. I have not addressed Paradox 2 very much because I think that another reviewer had solid and interesting comments on that front and I am leaving it to them. That being said, I do think Paradox 2 actually presents a deep problem in the literature and that the authors' argument may actually represent a path toward a solution.
This manuscript can be a useful contribution to the literature, but as it's presented at the moment, I think most of it is worded too strongly and it continues to not engage appropriately with the literature. Theoretical advances are undoubtedly important, and I think the manuscript presents some interesting things to think about, but ultimately needs to be better situated and several of the claims strongly toned down.
References:
Kaj, I., & Krone, S. M. (2003). The coalescent process in a population with stochastically varying size. Journal of Applied Probability, 40(1), 33-48. -

Reviewer #2 (Public review):
Summary:
This theoretical paper examines genetic drift in scenarios deviating from the standard Wright-Fisher model. The authors discuss Haldane's branching process model, highlighting that the variance in reproductive success equates to genetic drift. By integrating the Wright-Fisher model with the Haldane model, the authors derive theoretical results that resolve paradoxes related to effective population size.
Strengths:
The most significant and compelling result from this paper is perhaps that the probability of fixing a new beneficial mutation is 2s/V(K). This is an intriguing and potentially generalizable discovery that could be applied to many different study systems.
The authors also made a lot of effort to connect theory with various real-world examples, such as genetic diversity in sex chromosomes …
Reviewer #2 (Public review):
Summary:
This theoretical paper examines genetic drift in scenarios deviating from the standard Wright-Fisher model. The authors discuss Haldane's branching process model, highlighting that the variance in reproductive success equates to genetic drift. By integrating the Wright-Fisher model with the Haldane model, the authors derive theoretical results that resolve paradoxes related to effective population size.
Strengths:
The most significant and compelling result from this paper is perhaps that the probability of fixing a new beneficial mutation is 2s/V(K). This is an intriguing and potentially generalizable discovery that could be applied to many different study systems.
The authors also made a lot of effort to connect theory with various real-world examples, such as genetic diversity in sex chromosomes and reproductive variance across different species.
Comments on previous revisions:
The author has addressed some of the concerns in my review, and I think the revised manuscript is more clear. I like the discussion about the caveats of the WFH model.
I hope the authors could also discuss the conditions needed for V(K)/Ne to be a reasonable approximation. It is currently unclear how the framework should be adopted in general.
The idea about estimating male-female V(K) ratios from population genetic data is interesting. Unfortunately, the results fell short. The accuracy of their estimators (derived using approximation Ne/V(K) approximation, and certain choice of theta, and then theta estimated with Watterson's estimator) should be tested with simulated results before applying to real data. The reliability of their estimator and their results from real data are unclear.
Arguments made in this paper sometimes lack precision (perhaps the authors want to emphasize intuition, but it seems more confusing than otherwise). For example: The authors stated that "This independence from N seems intuitively obvious: when an advantageous mutation increases to say, 100 copies in determining a population (depending mainly on s), its fixation would be almost certain, regardless of N.". Assuming large Ne, and with approximation, one could assume the probability of loss is e^(-2sn), but the writing about "100 copies" and "almost certain" is very imprecise, in fact, a mutation with s=0.001 segregating at 100 copies in a large Ne population is most probably lost. Whereas in a small population, it will be fixed. Yet the following sentence states "regardless of N. This may be a most direct argument against equating genetic drift, certainly no less important than 1/ N . with N, or Ne (which is supposed to be a function of N's)." I find this new paragraph misleading.
Some of the statements/wordings in this paper still seem too strong to me.
Comments on revisions:
The authors toned down. I am a bit confused because I do not seem to find any point-to-point response to my review.
-

Reviewer #3 (Public review):
Summary:
Ruan and colleagues consider a branching process model (in their terminology the "Haldane model") and the most basic Wright-Fisher model. They convincingly show that offspring distributions are usually non-Poissonian (as opposed to what's assumed in the Wright-Fisher model), and can depend on short-term ecological dynamics (e.g., variance in offspring number may be smaller during exponential growth). The authors discuss branching processes and the Wright-Fisher model in the context of 3 "paradoxes" --- 1) how Ne depends on N might depend on population dynamics; 2) how Ne is different on the X chromosome, the Y chromosome, and the autosomes, and these differences do match the expectations base on simple counts of the number of chromosomes in the populations; 3) how genetic drift interacts with …
Reviewer #3 (Public review):
Summary:
Ruan and colleagues consider a branching process model (in their terminology the "Haldane model") and the most basic Wright-Fisher model. They convincingly show that offspring distributions are usually non-Poissonian (as opposed to what's assumed in the Wright-Fisher model), and can depend on short-term ecological dynamics (e.g., variance in offspring number may be smaller during exponential growth). The authors discuss branching processes and the Wright-Fisher model in the context of 3 "paradoxes" --- 1) how Ne depends on N might depend on population dynamics; 2) how Ne is different on the X chromosome, the Y chromosome, and the autosomes, and these differences do match the expectations base on simple counts of the number of chromosomes in the populations; 3) how genetic drift interacts with selection. The authors provide some theoretical explanations for the role of variance in the offspring distribution in each of these three paradoxes. They also perform some experiments to directly measure the variance in offspring number, as well as perform some analyses of published data.
Strengths:
- The theoretical results are well-described and easy to follow.
- The analyses of different variances in offspring number (both experimentally and analyzing public data) are convincing that non-Poissonian offspring distributions are the norm.
- The point that this variance can change as the population size (or population dynamics) change is also very interesting and important to keep in mind.
- I enjoyed the Density-Dependent Haldane model. It was a nice example of the decoupling of census size and effective size.
- Equation (10) is a nice resultComments on revisions:
I appreciate the effort that the authors have put into the revision, but I still find the framing to be a bit confusing -- these apparent paradoxes only appear in the most basic version of Wright-Fisher models, and so framing the paper as the solution to these paradoxes overlooks much previous work. Saying that existing work discussing exactly these phenomena is "beyond the scope of this study", without citing or interacting in any way with that work is unscholarly. I agree with the authors that the apparent paradoxes that they consider and interesting, and by thinking about branching processes, the apparent paradoxes appear to be less paradoxical, but without contextualizing this work in the substantial Wright-Fisher literature (e.g., Cannings Exchangeable Models and the work of Möhle) it misrepresents the state of the field and the contributions of this paper.
-

Author response:
The following is the authors’ response to the previous reviews.
eLife Assessment (divided into 3 parts)
This study presents a useful modification of a standard model of genetic drift by incorporating variance in reproductive success, claiming to address several paradoxes in molecular evolution. ……
It is crucial to emphasize that our model is NOT a modification of the standard model. The Haldane model, which is generalized here for population regulation, is based on the branching process. The Haldane model and the WF model which is based on population sampling are fundamentally different. We referred to our model as the integrated WF-H model because the results obtained from the WF model over the last 90 years are often (but not always) good approximations for the Haldane model. The analogy would be the comparisons …
Author response:
The following is the authors’ response to the previous reviews.
eLife Assessment (divided into 3 parts)
This study presents a useful modification of a standard model of genetic drift by incorporating variance in reproductive success, claiming to address several paradoxes in molecular evolution. ……
It is crucial to emphasize that our model is NOT a modification of the standard model. The Haldane model, which is generalized here for population regulation, is based on the branching process. The Haldane model and the WF model which is based on population sampling are fundamentally different. We referred to our model as the integrated WF-H model because the results obtained from the WF model over the last 90 years are often (but not always) good approximations for the Haldane model. The analogy would be the comparisons between the Diffusion model and the Coalescence model. Obviously, the results from one model are often good approximations for the other. But it is not right to say that one is a useful modification of the other.
We realize that it is a mistake to call our model the integrated WFH model, thus causing confusions over two entirely different models. Clearly, the word “integrated” did not help. We have now revised the paper by using the more accurate name for the model – the Generalized Haldane (GH) model. The text explains clerarly that the original Haldane model is a special case of the GH model.
Furthermore, we present the paradoxes and resolve them by the GH model. We indeed overreached by claiming that WF models could not resolve them. Whether the WF models have done enough to resolve the paradoxes or at least will be able to resolve them should not be a central point of our study. Here is what we state at the end of this study.:
“We understand that further modifications of the WF models may account for some or all of these paradoxes. However, such modifications have to be biologically feasible and, if possible, intuitively straightforward. Such possible elaborations of WF models are beyond the scope of this study. We are only suggesting that the Haldane model can be extensively generalized to be an alternative approach to genetic drift. The GH model attempts to integrate population genetics and ecology and, thus, can be applied to genetic systems far more complex than those studied before. The companion study is one such example.”
….. However, some of the claimed "paradoxes" seem to be overstatements, as previous literature has pointed out the limitations of the standard model and proposed more advanced models to address those limitations….
As stated in the last paragraph of the paper, it is outside of the scope of our study to comment on whether the earlier WF models can resolve these paradoxes. So, all such statements have been removed or at least drastically toned down in the formal presentation. That said, editors and reviewers may ask whether we are re-inventing the wheels. The answers are as follows:
First, two entirely different models reaching the same conclusion are NOT the re-invention of wheels. The coalescence theory does not merely rediscover the results obtained by the diffusion models. The process of obtaining the results is itself a new invention. This would lead to the next question: is the new process more rigorous and more efficient? I think the Haldane model is indeed more efficient in comparisons with the very complex modifications of the WF models.
Second, we are not sure that the paradoxes have been resolved, or even can be resolved. Note that these skepticisms have been purged from the formal presentation. Thefore, I am presenting the arguments outside of the paper for a purely intellectual discourse. Below, please allow us to address the assertions that the WF models can resolve the paradoxes.
The first paradox is that the drift strength in relation to N is often opposite of the WF model predictions. Since the WF models (standard or modified) do not generate N from within the model, how can it resolve the paradox? In contrast, the Generalized Haldane model generates N within the model. It is the regulation of N near the carrying capacity that creates the paradox – When N increases, drift also increases.
The second paradox that the same locus experiences different drifts in males and females is accepted by the reviewers. Nevertheless, we would like to point out that this second paradox echoed the first one as newly stated in the Discussion section “The second paradox of sex-dependent drift is about different V(K)’s between sexes (generally Vm > Vf) but the same E(K) between them. In the conventional models of sampling, it is not clear what sort of biological sampling scheme could yield V(K) ≠ E(K), let alone two separate V(K)’s with one single E(K). Mathematically, given separate K distributions for males and females, it is unlikely that E(K) for the whole population could be 1, hence, the population would either explode in size or decline to zero. In short, N regulation has to be built into the genetic drift model as the GH model does to avoid this paradox.”
The third paradox stems from the fact that drift is operating even for genes under selection. But then the drift strength, 2s/V(K) for an advantage of s, is indepenent of N or Ne. Since the determinant of drift strength in the WF model is ALWAYS Ne, how is Paradox 3 not a paradox for the WF model?
The 4th paradox about multi-copy gene systems is the subject of the companion paper (Wang et al.). Note that the WF model cannot handle systems of evolution that experience totally different sorts of drift within vs. between hosts (viruses, rDNAs etc). This paradox can be understood by the GH model and and will be addressed in the next paper.
While the modified model presented in this paper yields some intriguing theoretical predictions, the analysis and simulations presented are incomplete to support the authors' strong claims, and it is unclear how much the model helps explain empirical observations.
The objections appear to be that our claims of “paradox resolution” being too strong. We interpret this objection is based on the view (which we agree) that these paradoxes are intrisicallly difficult to resolve by the WF models. Since our model has been perceived to be a modified WF model, the claim of resolution is clearly too strong. However, the GH model is conceptually and operationally entirely different from the WF models as we have emphasized above. In case our reading of the editorial comments is incorrect, would it be possible for some clarifications on the nature of “incomplete support”? We would be grateful for the help.
-

-

-

-

eLife Assessment
This study presents a useful model of genetic drift by incorporating variance in reproductive success, claiming to address several paradoxes in molecular evolution. However, some of the claimed "paradoxes" seem to be overstatements, as previous literature has pointed out the limitations of the standard model and proposed more advanced models to address those limitations. While the proposed new model presented in this paper yields some intriguing theoretical predictions, the analysis and simulations presented are incomplete to support the authors' strong claims, and it is unclear how much the model helps explain empirical observations.
-

Reviewer #1 (Public review):
The revision by Ruan et al clarifies several aspects of the original manuscript that were difficult to understand, and I think it presents some useful and interesting ideas. I understand that the authors are distinguishing their model from the standard Wright-Fisher model in that the population size is not imposed externally, but is instead a consequence of the stochastic reproduction scheme. Here, the authors chose a branching process but in principle any Markov chain can probably be used. Within this framework, the authors are particularly interested in cases where the variance in reproductive success changes through time, as explored by the DDH model, for example. They argue with some experimental results that there is a reason to believe that the variance in reproductive success does change over time.
One…
Reviewer #1 (Public review):
The revision by Ruan et al clarifies several aspects of the original manuscript that were difficult to understand, and I think it presents some useful and interesting ideas. I understand that the authors are distinguishing their model from the standard Wright-Fisher model in that the population size is not imposed externally, but is instead a consequence of the stochastic reproduction scheme. Here, the authors chose a branching process but in principle any Markov chain can probably be used. Within this framework, the authors are particularly interested in cases where the variance in reproductive success changes through time, as explored by the DDH model, for example. They argue with some experimental results that there is a reason to believe that the variance in reproductive success does change over time.
One of the key aspects of the original manuscript that I want to engage with is the DDH model. As the authors point out, their equations 5 and 6 are assumptions, and not derived from any principles. In essence, the authors are positing that that the variance in reproductive success, given by 6, changes as a function of the current population size. There is nothing "inherent" to a negative binomial branching mechanism that results in this: in fact, the the variance in offspring number could in principle be the same for all time. As relates to models that exist in the literature, I believe that this is the key difference: unlike Cannings models, the authors allow for a changing variance in reproduction through time.
This is, of course, an interesting thing to consider, and I think that the situation the authors point out, in which drift is lower at small population sizes and larger at large population sizes, is not appreciated in the literature. However, I am not so sure that there is anything that needs to be resolved in Paradox 1. A very strong prediction of that model is that Ne and N could be inversely related, as shown by the blue line in Fig 3b. This suggests that you could see something very strange if you, for example, infer a population size history using a Wright-Fisher framework, because you would infer a population *decline* when there is in fact a population *expansion*. However, as far as I know there are very few "surprising population declines" found in empirical data. An obvious case where we know there is very rapid population growth is human populations; I don't think I've ever seen an inference of recent human demographic history from genetic data that suggests anything other than a massive population expansion. While I appreciate the authors empirical data supporting their claim of Paradox 1 (more on the empirical data later), it's not clear to me that there's a "paradox" in the literature that needs explaining so much as this is a "words of caution about interpreting inferred effective population sizes". To be clear, I think those words of caution are important, and I had never considered that you might be so fundamentally misled as to infer decline when there is growth, but calling it a "paradox" seems to suggest that this is an outstanding problem in the literature, when in fact I think the authors are raising a *new* and important problem. Perhaps an interesting thing for the authors to do to raise the salience of this point would be to perform simulations under this model and then infer effective population sizes using e.g. dadi or psmc and show that you could identify a situation in which the true history is one of growth, but the best fit would be one of decline
The authors also highlight that their approach reflects a case where the population size is determined by the population dynamics themselves, as opposed to being imposed externally as is typical in Cannings models. I agree with the authors that this aspect of population regulation is understudied. Nonetheless, several manuscripts have dealt with the case of population genetic dynamics in populations of stochastically fluctuating size. For example, Kaj and Krone (2003) show that under pretty general conditions you get something very much like a standard coalescent; for example, combining their theorem 1 with their arguments on page 36 and 37, they find that exchangeable populations with stochastic population dynamics where the variance does not change with time still converge to exactly the coalescent you would expect from Cannings models. This is strongly suggestive that the authors key result isn't about stochastic population dynamics per se, but instead related to arguing that variance in reproductive success could change through time. In fact, I believe that the result of Kaj and Krone (2003) is substantially more general than the models considered in this manuscript. That being said, I believe that the authors of this manuscript do a much better job of making the implications for evolutionary processes clear than Kaj and Krone, which is important---it's very difficult to understand from Kaj and Krone the conditions under which effective population sizes will be substantially impacted by stochastic population dynamics.
I also find the authors exposition on Paradox 3 to be somewhat strange. First of all, I'm not sure there's a paradox there at all? The authors claim that the lack of dependence of the fixation probability on Ne is a paradox, but this is ultimately not surprising---fixation of a positively selected allele depends mostly on escaping the boundary layer, which doesn't really depend on the population size (see Gillespie's book "The Causes of Molecular Evolution" for great exposition on boundary layer effects). Moreover, the authors *use a Cannings-style argument* to get gain a good approximation of how the fixation probability changes when there is non-Poisson reproduction. So it's not clear that the WFH model is really doing a lot of work here. I suppose they raise the interesting point that the particularly simple form of p(fix) = 2s is due to the assumption that variance in offspring is equal to 1.
In addition, I raised some concerns about the analysis of empirical results on reproductive variance in my original review, and I don't believe that the authors responded to it at all. I'm not super worried about that analysis, but I think that the authors should probably respond to me.
Overall, I feel like I now have a better understanding of this manuscript. However, I think it still presents its results too strongly: Paradox 1 contains important words of caution that reflect what I am confident is an under appreciated possibility, and Paradox 3 is, as far as I'm concerned, not a paradox at all. I have not addressed Paradox 2 very much because I think that another reviewer had solid and interesting comments on that front and I am leaving it to them. That being said, I do think Paradox 2 actually presents a deep problem in the literature and that the authors' argument may actually represent a path toward a solution.
This manuscript can be a useful contribution to the literature, but as it's presented at the moment, I think most of it is worded too strongly and it continues to not engage appropriately with the literature. Theoretical advances are undoubtedly important, and I think the manuscript presents some interesting things to think about but ultimately needs to be better situated and several of the claims strongly toned down.
References:
Kaj, I., & Krone, S. M. (2003). The coalescent process in a population with stochastically varying size. Journal of Applied Probability, 40(1), 33-48. -

Reviewer #2 (Public review):
Summary:
This theoretical paper examines genetic drift in scenarios deviating from the standard Wright-Fisher model. The authors discuss Haldane's branching process model, highlighting that the variance in reproductive success equates to genetic drift. By integrating the Wright-Fisher model with the Haldane model, the authors derive theoretical results that resolve paradoxes related to effective population size.
Strengths:
The most significant and compelling result from this paper is perhaps that the probability of fixing a new beneficial mutation is 2s/V(K). This is an intriguing and potentially generalizable discovery that could be applied to many different study systems.
The authors also made a lot of effort to connect theory with various real-world examples, such as genetic diversity in sex chromosomes …
Reviewer #2 (Public review):
Summary:
This theoretical paper examines genetic drift in scenarios deviating from the standard Wright-Fisher model. The authors discuss Haldane's branching process model, highlighting that the variance in reproductive success equates to genetic drift. By integrating the Wright-Fisher model with the Haldane model, the authors derive theoretical results that resolve paradoxes related to effective population size.
Strengths:
The most significant and compelling result from this paper is perhaps that the probability of fixing a new beneficial mutation is 2s/V(K). This is an intriguing and potentially generalizable discovery that could be applied to many different study systems.
The authors also made a lot of effort to connect theory with various real-world examples, such as genetic diversity in sex chromosomes and reproductive variance across different species.
Comments on revisions:
The author has addressed some of the concerns in my review, and I think the revised manuscript is more clear. I like the discussion about the caveats of the WFH model.
I hope the authors could also discuss the conditions needed for V(K)/Ne to be a reasonable approximation. It is currently unclear how the framework should be adopted in general.
The idea about estimating male-female V(K) ratios from population genetic data is interesting. Unfortunately, the results fell short. The accuracy of their estimators (derived using approximation Ne/V(K) approximation, and certain choice of theta, and then theta estimated with Watterson's estimator) should be tested with simulated results before applying to real data. The reliability of their estimator and their results from real data are unclear.
Arguments made in this paper sometimes lack precision (perhaps the authors want to emphasize intuition, but it seems more confusing than otherwise). For example: The authors stated that "This independence from N seems intuitively obvious: when an advantageous mutation increases to say, 100 copies in determining a population (depending mainly on s), its fixation would be almost certain, regardless of N.". Assuming large Ne, and with approximation, one could assume the probability of loss is e^(-2sn), but the writing about "100 copies" and "almost certain" is very imprecise, in fact, a mutation with s=0.001 segregating at 100 copies in a large Ne population is most probably lost. Whereas in a small population, it will be fixed. Yet the following sentence states "regardless of N. This may be a most direct argument against equating genetic drift, certainly no less important than 1/ N . with N, or Ne (which is supposed to be a function of N's)." I find this new paragraph misleading.
Some of the statements/wordings in this paper still seem too strong to me.
-

Reviewer #3 (Public review):
Summary:
Ruan and colleagues consider a branching process model (in their terminology the "Haldane model") and the most basic Wright-Fisher model. They convincingly show that offspring distributions are usually non-Poissonian (as opposed to what's assumed in the Wright-Fisher model), and can depend on short-term ecological dynamics (e.g., variance in offspring number may be smaller during exponential growth). The authors discuss branching processes and the Wright-Fisher model in the context of 3 "paradoxes" --- 1) how Ne depends on N might depend on population dynamics; 2) how Ne is different on the X chromosome, the Y chromosome, and the autosomes, and these differences do match the expectations base on simple counts of the number of chromosomes in the populations; 3) how genetic drift interacts with …
Reviewer #3 (Public review):
Summary:
Ruan and colleagues consider a branching process model (in their terminology the "Haldane model") and the most basic Wright-Fisher model. They convincingly show that offspring distributions are usually non-Poissonian (as opposed to what's assumed in the Wright-Fisher model), and can depend on short-term ecological dynamics (e.g., variance in offspring number may be smaller during exponential growth). The authors discuss branching processes and the Wright-Fisher model in the context of 3 "paradoxes" --- 1) how Ne depends on N might depend on population dynamics; 2) how Ne is different on the X chromosome, the Y chromosome, and the autosomes, and these differences do match the expectations base on simple counts of the number of chromosomes in the populations; 3) how genetic drift interacts with selection. The authors provide some theoretical explanations for the role of variance in the offspring distribution in each of these three paradoxes. They also perform some experiments to directly measure the variance in offspring number, as well as perform some analyses of published data.
Strengths:
- The theoretical results are well-described and easy to follow.
- The analyses of different variances in offspring number (both experimentally and analyzing public data) are convincing that non-Poissonian offspring distributions are the norm.
- The point that this variance can change as the population size (or population dynamics) change is also very interesting and important to keep in mind.
- I enjoyed the Density-Dependent Haldane model. It was a nice example of the decoupling of census size and effective size.
- Equation (10) is a nice result (but see below)Weaknesses:
- I am not convinced that these types of effects cannot just be absorbed into some time-varying Ne and still be well-modeled by the Wright-Fisher process. As a concrete example, Mohle and Sagitov 2001 show that a "coalescent Ne" for the WF model should be (N-1)/Var(K). This resolves the exponentially growing bacteria "paradox" raised in the present paper --- when the bacteria are growing Var(K) ~ 0, and hence there should be very little drift. This exactly resolves the "paradox" raised by the authors. Instead, it merely underscores that Ne does not need to be equal to (or even positively correlated!) with N. I absolutely do not see this as a failure of the WF model. Whether one finds branching processes or the WF model more biologically intuitive is a matter of taste, but to say that WF models cannot explain this "paradox" is false, when a well-known paper from more than 20 years ago does just that.
- Along these lines, the result that Ne in the Wright-Fisher process might not be related to N in any straightforward (or even positively correlated) way are well-known (e.g., Neher and Hallatschek 2012; Spence, Kamm, and Song 2016; Matuszewski, Hildebrandt, Achaz, and Jensen 2018; Rice, Novembre, and Desai 2018; the work of Lounès Chikhi on how Ne can be affected by population structure; etc...)
- I was also missing some discussion of the relationship between the branching process and the Wright-Fisher model (or more generally Cannings' Exchangeable Models) when conditioning on the total population size. In particular, if the offspring distribution is Poisson, then conditioned on the total population size, the branching process is identical to the Wright-Fisher model.
- Given that Cannings' exchangeable models decouple N and Ne, it would not surprise me if something like equation (10) could be derived under such a model. I have not seen such a derivation, and the authors' result is nice, but I do not see it as proof that WF-type models (i.e., Cannings' models) are irreparably broken. -

Author response:
The following is the authors’ response to the original reviews.
eLife Assessment
This study presents a useful modification of a standard model of genetic drift by incorporating variance in offspring numbers, claiming to address several paradoxes in molecular evolution. It is unfortunate that the study fails to engage prior literature that has extensively examined the impact of variance in offspring number, implying that some of the paradoxes presented might be resolved within existing frameworks.
The prior literature the reviewers referred to are all "modified WF models". In the original submission, we lumped the standard and modified WF models together as the "generalized WF models". As the lumping causes confusions, their distinctions are now made clear. That said, the Haldane model in our proposal is not a …
Author response:
The following is the authors’ response to the original reviews.
eLife Assessment
This study presents a useful modification of a standard model of genetic drift by incorporating variance in offspring numbers, claiming to address several paradoxes in molecular evolution. It is unfortunate that the study fails to engage prior literature that has extensively examined the impact of variance in offspring number, implying that some of the paradoxes presented might be resolved within existing frameworks.
The prior literature the reviewers referred to are all "modified WF models". In the original submission, we lumped the standard and modified WF models together as the "generalized WF models". As the lumping causes confusions, their distinctions are now made clear. That said, the Haldane model in our proposal is not a modification of the standard WF model because, conceptually, the two models are very different. WF is based on sampling whereas the Haldane model is based on gene transmission.
While the "modified WF models" often incorporate V(K) [variance in progeny number], the modification is still based on the WF model of population sampling. The modification is mathematically feasible but biologically untenable, as explained explicitly in the revised text. Most important, all four paradoxes are as incompatible with the modified WF models as with the standard model. Note that the Haldane model does not have the sampling step, which is absorbed into the V(K) term. In the integrated WF-Haldane model, these paradoxes are resolved (see the new sections of Discussion, quoted below).
If readers do not have time to ponder on all four paradoxes, they may simply read the first one, as follows. When the population size (N) is growing exponentially, such as in a bacteria culture, drift is nearly absent when N is small and becomes stronger as N increases, especially when approaching the carrying capacity. Such common observations are exactly opposite of the WF model's central prediction. Any model based on sampling cannot escape the constraint of "greater drift, smaller N".
Revision - The following text is a reproduction of the last 7 paragraphs of Discussion.
“The standard WF model has been extended in several directions (overlapping generations, multiple alleles, ploidy, etc.). The modification most relevant to our studies here is the introduction of V(K) into the model, thus permitting V(K) ≠ E(K). While the modifications are mathematically valid, they are often biologically untenable. Kimura and Crow (1963) may be the first to offer a biological mechanism for V(K) ≠ E(K), effectively imposing the Haldane model on the WF model. Other models (Kimura and Crow 1963; Lynch, et al. 1995; Sjodin, et al. 2005; Der, et al. 2011; Cannings 2016) indeed model mathematically the imposition of the branching process on the population, followed by the WF sampling. The constructions of such models are biologically dubious but, more importantly, still unable to resolve the paradoxes. It would seem more logical to use the Haldane model in the first place by having two parameters, E(K) and V(K).
Even if we permit V(K) ≠ E(K) under the WF sampling, the models would face other difficulties. For example, a field biologist needs to delineate a Mendelian population and determine its size, N or Ne. In all WF models, one cannot know what the actual population being studied is. Is it the fly population in an orchard being sampled, in the geographical region, or in the entire species range? It is unsatisfactory when a population biologist cannot identify the population being studied. The Haldane model is an individual-output model (Chen, et al. 2017), which does not require the delineation of a Mendelian population.
We shall now review the paradoxes specifically in relation to the modified WF models, starting with the multi-copy gene systems such as viruses and rRNA genes covered in the companion study (Wang, et al. 2024). These systems evolve both within and between hosts. Given the small number of virions transmitted between hosts, drift is strong in both stages as shown by the Haldane model (Ruan, Luo, et al. 2021; Ruan, Wen, et al. 2021; Hou, et al. 2023). Therefore, it does not seem possible to have a single effective population size in the WF models to account for the genetic drift in two stages. The inability to deal with multi-copy gene systems may explain the difficulties in accounting for the SARS-CoV-2 evolution (Deng, et al. 2022; Pan, Liu, et al. 2022; Ruan, Wen, et al. 2022; Hou, et al. 2023; Ruan, et al. 2023).
We now discuss the first paradox of this study, which is about the regulation of N. In the general WF models, N is imposed from outside of the model, rather than self-generating within the model. When N is increasing exponentially as in bacterial or yeast cultures, there is almost no drift when N is very low and drift becomes intense as N grows to near the carrying capacity. As far as we know, no modifications of the WF model can account for this phenomenon that is opposite of its central tenet. In the general WF models, N is really the carrying capacity, not population size.
The second paradox of sex chromosomes is rooted in V(K) ≠ E(K). As E(K) is the same between sexes but V(K) is different, clearly V(K) = E(K) would not be feasible. The mathematical solution of defining separate Ne's for males and females (Kimura and Crow 1963; Lynch, et al. 1995; Sjodin, et al. 2005; Der, et al. 2011; Cannings 2016) unfortunately obscures the interesting biology. As shown in Wang et al. (2024; MBE), the kurtosis of the distribution of K indicates the presence of super-breeder males. While the Haldane model can incorporate the kurtosis, the modified WF models are able to absorb only up to the variance term, i.e., the second moment of the distribution. The third paradox of genetic drift is manifested in the fixation probability of an advantageous mutation, 2_s_/V(K). As explained above, the fixation probability is determined by the probability of reaching a low threshold that is independent of N itself. Hence, the key parameter of drift in the WF model, N (or Ne), is missing. This paradox supports the assertion that genetic drift is fundamentally about V(K) with N being a scaling factor.
As the domain of evolutionary biology expands, many new systems do not fit into the WF models, resulting in the lack of a genetic drift component in their evolutionary trajectories. Multi-copy gene systems are obvious examples. Others include domestications of animals and plants that are processes of rapid evolution (Diamond 2002; Larson and Fuller 2014; Purugganan 2019; Chen, Yang, et al. 2022; Pan, Zhang, et al. 2022; Wang, et al. 2022). Due to the very large V(K) in domestication, drift must have played a large role. Somatic cell evolution is another example with “undefinable” genetic drift (Wu, et al. 2016; Chen, et al. 2017; Chen, et al. 2019; Ruan, et al. 2020; Chen, Wu, et al. 2022). The Haldane (or WFH) model, as an "individual output" model, can handle these general cases of genetic drift.
The Haldane model and the WF model are fundamentally different approaches to random forces of evolution. While the WF models encounter many biological contradictions, they have provided approximate mathematical solutions to more realistic scenarios. In systems such as in viral evolution (Ruan, Hou, et al. 2022; Hou, et al. 2023) or somatic cell evolution (Chen, Wu, et al. 2022; Zhai, et al. 2022) whereby the WF solution is absent, further development of the WFH model will be necessary.”
In addition, while the modified model yields intriguing theoretical predictions, the simulations and empirical analyses are incomplete to support the authors' claims.
This point is addressed in the responses to reviewers' comments. Since they are quite technical, they do not fit in the overview here.
Public Reviews:
Reviewer #1 (Public Review):
Summary:
The authors present a theoretical treatment of what they term the "Wright-Fisher-Haldane" model, a claimed modification of the standard model of genetic drift that accounts for variability in offspring number, and argue that it resolves a number of paradoxes in molecular evolution. Ultimately, I found this manuscript quite strange.
The notion of effective population size as inversely related to the variance in offspring number is well known in the literature, and not exclusive to Haldane's branching process treatment. However, I found the authors' point about variance in offspring changing over the course of, e.g. exponential growth fairly interesting, and I'm not sure I'd seen that pointed out before.
Weaknesses:
I have several outstanding issues. First of all, the authors really do not engage with the literature regarding different notions of an effective population. Most strikingly, the authors don't talk about Cannings models at all, which are a broad class of models with non-Poisson offspring distributions that nonetheless converge to the standard Wright-Fisher diffusion under many circumstances, and to "jumpy" diffusions/coalescents otherwise (see e.g. Mohle 1998, Sagitov (2003), Der et al (2011), etc.). Moreover, there is extensive literature on effective population sizes in populations whose sizes vary with time, such as Sano et al (2004) and Sjodin et al (2005).
Of course in many cases here the discussion is under neutrality, but it seems like the authors really need to engage with this literature more.
The reviewer's summary and weakness statement reflects the general criticism summarized by the editors. The reply and revision to these criticisms have been presented in the long reply to elife assessment above.
We hence re-emphasize only the key points here.
(1) The literature that the reviewers fault us for not citing is about the modifications of the standard WF model. We now cite them as well as a few others in that vein. However, the WF-Haldane model we propose is conceptually very different from the modified WF models. This WFH model is in essence the Haldane model which may use the results of the WF models as the starting point to find the exact solutions.
(2) The check of the power of the modified WF models is whether they can resolve the paradoxes. None of them can. The arguments apply to neutral cases as well as selection effects. Hence, our central point is that the modifications of the standard WF model [e.g., by incorporating V(K)] do not help the WF model in resolving the paradoxes. Besides, the incorporation of V(K) is mathematically feasible but biologically untenable as presented in the new sections of Discussion.
Nonetheless, I don't think the authors' modeling, simulations, or empirical data analysis are sufficient to justify their claims.
The most interesting part of the manuscript, I think, is the discussion of the Density Dependent Haldane model (DDH). However, I feel like I did not fully understand some of the derivation presented in this section, …… - this is the whole notion of exchangeability, also neglected in this manuscript). As such, I don't believe that their analysis of the empirical data supports their claim. [Since the comments above are highly technical and fairly long, they are not copied verbatim.]
We thank this reviewer for the detailed comments with respect to the potential confusion in the discussion of the Density Dependent Haldane (DDH) model.
First, the reviewer appears to ask how Eqs (5-6) are derived. We should clarify that both Eq (5) and (6) are assumptions rather than derived results. Both equations are assumptions based on population ecology. Eq (7) is then derived by substituting the assumptions in Eq (5) and (6) into Eq (3).
The definition in Equation (5) allows the growth rate of the population size to be dependent on N itself, such that growth rate E(K) (average offspring number per generation) is greater than 1 when N < Ck and less than 1 when N > Ck. The parameter z is introduced to adjust the sensitivity of E(K) to changes in population size (as shown in Fig. 3a).
Second, we appreciate the comments regarding the use of individual-based simulations and the apparent lack of interaction between individuals. In our simulations, there is indeed an interaction among individuals, which is represented by Eq (5). This equation reflects how the competition between two alleles affects the expected growth rate 𝐸(𝐾), which decreases as the population size increases. Furthermore, once 𝐸(𝐾) for the entire population is determined, the offspring numbers of the alleles are independent.
We believe that the primary purpose of our simulations was not clearly stated. This lack of clarity may be the root of the criticisms. We now note that the simulations are aimed at testing the accuracy of Equation (10).
Note that Eq. (10) is a textbook result and quite important in our study. This equation shows that the strength of genetic drift, as given by Pf (the fixation probability of an advantageous mutation), is not a function of N at all. This approximate solution has been obtained using the WF model by Kimura. The Haldane model solution that can explain Paradox 1 is based on Equation (7) as shown below
Since the fixation probability of Equation (10) cannot be easily obtained using Eq. (7), we conducted simulations to confirm the accuracy of Eq. (10) when applied to the Haldane model.
We have revised the relevant sections of the manuscript to clarify these points and to better distinguish between assumptions and results.
Revision - Details of the DDH model are given in the Supplementary Information. A synopsis is given here: We consider a non-overlapping haploid population with two neutral alleles. The population size at time t is Nt. We assume that expected growth rate E(K) is greater than 1 when N < Ck and less than 1 when N > Ck, as defined by Eq. (5) below:
The slope of E(K) vs. N (i.e., the sensitive of growth rate to changes in population size), as shown in Fig 3a, depends on z. To determine the variance V(K), we assume that K follows the negative binomial distribution whereby parents would suffer reproduction-arresting injury with a probability of pt at each birthing (Supplementary Information). Accordingly, V(K) can then be expressed as
By Eq. (6), the ratio of V(K)/E(K) could be constant, decrease or increase with the increase of population size. With E(K) and V(K) defined, we could obtain the effective population size by substituting Eq. (5) and Eq. (6) into Eq. (3).
Eq. (7) presents the relationship between effective population size (Ne) and the population size (N) as shown in Fig. 3. The density-dependent E(K) could regulate N with different strength (Fig. 3a). The steeper the slope in Fig. 3a, the stronger the regulation.
Simulation of genetic drift in the Haldane model and the Wright-Fisher (WF) model. In both models, interactions between individuals are implicitly included through the dependency of the average number of offspring on population size, as defined by Eq. (5). This dependency leads to the logistic population growth, reflecting the density-dependent interactions.
Thus, while I think there are some interesting ideas in this manuscript, I believe it has some fundamental issues:
first, it fails to engage thoroughly with the literature on a very important topic that has been studied extensively. Second, I do not believe their simulations are appropriate to show what they want to show. And finally, I don't think their empirical analysis shows what they want to show.
References omitted
The comments are the summary of previous ones, which have been addressed in detail in the preceding sections.
Reviewer #2 (Public Review):
Summary:
This theoretical paper examines genetic drift in scenarios deviating from the standard Wright-Fisher model. The authors discuss Haldane's branching process model, highlighting that the variance in reproductive success equates to genetic drift. By integrating the Wright-Fisher model with the Haldane model, the authors derive theoretical results that resolve paradoxes related to effective population size [Ne]
Thanks. The issue of Ne will be addressed below where the reviewer returns to this issue. The strength of the integrated WFH model is that N (or Ne) is generated by the model itself, rather than externally imposed as in WF models.
Strengths:
The most significant and compelling result from this paper is perhaps that the probability of fixing a new beneficial mutation is 2s/V(K). This is an intriguing and potentially generalizable discovery that could be applied to many different study systems.
The authors also made a lot of effort to connect theory with various real-world examples, such as genetic diversity in sex chromosomes and reproductive variance across different species.
Thanks.
Weaknesses:
One way to define effective population size is by the inverse of the coalescent rate. This is where the geometric mean of Ne comes from. If Ne is defined this way, many of the paradoxes mentioned seem to resolve naturally. If we take this approach, one could easily show that a large N population can still have a low coalescent rate depending on the reproduction model. However, the authors did not discuss Ne in light of the coalescent theory. This is surprising given that Eldon and Wakeley's 2006 paper is cited in the introduction, and the multiple mergers coalescent was introduced to explain the discrepancy between census size and effective population size, superspreaders, and reproduction variance - that said, there is no explicit discussion or introduction of the multiple mergers coalescent.
The Haldane model treats N’s very differently from the WF models. In the WF models, N’s are imposed externally (say, constant N, exponentially growing N, temporally fluctuating N’s and so on; all provided from outside of the model). Ne and coalescence are all derived from these given N’s. In order to account for the first paradox (see the next paragraph), N needs to be regulated but the WF models cannot regulate N’s. The density-dependent Haldane model that Reviewer 1 inquired above is a model that regulates N internally. It can thus account for the paradox.
Paradox 1 - When the population size (N) is growing exponentially, such as in a bacteria culture, drift is nearly absent when N is small and is much stronger as N increases, especially when approaching the carrying capacity. Such a pattern is a common observation and is exactly opposite of the WF model's central prediction. In short, a model that does not regulate N cannot explain the paradox
Ne is a fix of the WF model in order to account for the missing components of genetic drift. The paradoxes presented in this one and the companion study show that the fix is rather inadequate. In contrast, by the WFH model, N is regulated within the model itself as E(K) and V(K) are both functions of N.
The Wright-Fisher model is often treated as a special case of the Cannings 1974 model, which incorporates the variance in reproductive success. This model should be discussed. It is unclear to me whether the results here have to be explained by the newly introduced WFH model, or could have been explained by the existing Cannings model. The abstract makes it difficult to discern the main focus of the paper. It spends most of the space introducing "paradoxes".
We appreciate greatly the illuminating advice. Nevertheless, we should explain, or should have explained, more clearly that these four paradoxes presented are central to this pair of eLife papers. The WF and Haldane models are very different conceptual ideas altogether. The choice should not be based on mathematical grounds but on how they help us understand biological evolution. We are using four paradoxes to highlight the differences. We have said in the papers that the origin and evolution of COVID-19 caused a lot of confusions partly because the WF models cannot handle multi-copy gene systems, including viruses that evolve both within- and between- hosts.
The standard Wright-Fisher model makes several assumptions, including hermaphroditism, non-overlapping generations, random mating, and no selection. It will be more helpful to clarify which assumptions are being violated in each tested scenario, as V(K) is often not the only assumption being violated. For example, the logistic growth model assumes no cell death at the exponential growth phase, so it also violates the assumption about non-overlapping generations.
We appreciate the question which has two aspects. First, why do we think the WF models are insufficient? After all, for each assumption of the WF model (as given in the reviewer’s examples), there is often a solution by modifying Ne which relaxes the assumption. In this sense, there is only one grand assumption made by the WF models. That is, however complex the biology is, it is possible to find Ne that can make the WF model work. Our argument is that Ne is a cumbersome fix of the WF model and it does not work in many situations. That is how we replied about the importance of the paradoxes above. We shall again use the first paradox as an example whereby drift is stronger as N becomes larger, the fix has to make Ne negatively correlated with N. In reality, it does not appear possible to resolve this paradox. Another paradox is the evolution of multi-copy gene systems. In short, it seems clear that Ne is not a useful or usable fix.
The second aspect is that “why, among the many modifications the WF models make, do we only emphasize the inclusion of V(K)?” This is the essence of the two papers of ours. Although V(K) is a modification of the WF models, it does not enable the WF models to resolve the paradoxes. In contrast, the Haldane model has incorporate E(K) and V(K) in the model. In presenting paradox 3, it was stated that
This equation shows that the strength of genetic drift, as given by Pf (the fixation probability of an advantageous mutation), is not a function of N at all. It supports the view that the essence of genetic drift is V(K) with N as a scaling factor. Note that, if V(K) = 0, there is no genetic drift regardless of N. As V(K) is not an add-on to the Haldane model (unlike in WF models), the Haldane model can resolve the paradoxes.
The theory and data regarding sex chromosomes do not align. The fact that \hat{alpha'} can be negative does not make sense. The authors claim that a negative \hat{alpha'} is equivalent to infinity, but why is that? It is also unclear how theta is defined. It seems to me that one should take the first principle approach e.g., define theta as pairwise genetic diversity, and start with deriving the expected pair-wise coalescence time under the MMC model, rather than starting with assuming theta = 4Neu. Overall, the theory in this section is not well supported by the data, and the explanation is insufficient.
a' can be negative for the same reason that a (the male/female ratio in mutation rate) can be negative (Miyata, et al. 1987; Li, et al. 2002; Makova and Li 2002). Clearly, this has not been a problem in the large literature on a becoming negative. In fact, in many reports, a is negative, which is read as a approaching infinity. Imagine that our equation is a'^2 = 0.25, then a' can be 0.5 or -0.5, although the latter solution is not biologically meaningful.
As for theta, the reviewer asked why we do not use the pairwise genetic diversity (or theta[pi]) as the first-principle approach to estimating theta. While theta(pi) is the first estimator of theta used, the general principle is that every bin of the frequency spectrum can be used for estimating theta since the expected value is theta/i where i is the occurrence of the mutation in the sample. (If the sample size is 100, then i is between 1 and 99.) Hence, the issue is which part of the spectrum has the best statistical properties for the questions at hand. The pairwise measure is theta(pi) [which the reviewer recommends]. While theta(pi) and theta(w) are most commonly used, there are in fact numerous ways to estimate theta. ((Fu 2022) presents an excellent review.) For our purpose, we need a theta estimate least affected by selection and we choose the lowest frequency bin of the spectrum, which is theta(1) based on the singletons. Theta(1), least affected by selection, is the basis of the Fu and Li test.
Reviewer #3 (Public Review):
Summary:
Ruan and colleagues consider a branching process model (in their terminology the "Haldane model") and the most basic Wright-Fisher model. They convincingly show that offspring distributions are usually non-Poissonian (as opposed to what's assumed in the Wright-Fisher model), and can depend on short-term ecological dynamics (e.g., variance in offspring number may be smaller during exponential growth). The authors discuss branching processes and the Wright-Fisher model in the context of 3 "paradoxes": (1) how Ne depends on N might depend on population dynamics; (2) how Ne is different on the X chromosome, the Y chromosome, and the autosomes, and these differences do match the expectations base on simple counts of the number of chromosomes in the populations; (3) how genetic drift interacts with selection. The authors provide some theoretical explanations for the role of variance in the offspring distribution in each of these three paradoxes. They also perform some experiments to directly measure the variance in offspring number, as well as perform some analyses of published data.
Strengths:
(1) The theoretical results are well-described and easy to follow.
(2) The analyses of different variances in offspring number (both experimentally and analyzing public data) are convincing that non-Poissonian offspring distributions are the norm.
(3) The point that this variance can change as the population size (or population dynamics) change is also very interesting and important to keep in mind.
(4) I enjoyed the Density-Dependent Haldane model. It was a nice example of the decoupling of census size and effective size.
Thanks.
Weaknesses:
(1) I am not convinced that these types of effects cannot just be absorbed into some time-varying Ne and still be well-modeled by the Wright-Fisher process.
Please allow us to refer to, again, two of the four paradoxes. We believe that that no modification of the WF model can resolve the paradoxes.
(1) When the population size (N) is growing exponentially, such as in a bacteria culture, drift is nearly absent when N is small and is much stronger as N increases, especially when approaching the carrying capacity. Such common observations are exactly opposite of the WF model's key prediction. It is not possible for a model that does not regulate N to explain the paradox.
(2) There is no way the WF models can formulate Ne for, say viruses or ribosomal RNA genes that have two levels of populations – the within-host populations as well as the host population itself.
The fact that there are numerous Ne's suggests that Ne is a collection of cumbersome fixes of the WF model. By the WF-Haldane model, all factors are absorbed into V(K) resulting in a simpler model in the end. V(K) is often a measurable quantity. Note that, even if V(K) is incorporated into the WF model, the paradoxes remain unresolvable.
(2) Along these lines, there is well-established literature showing that a broad class of processes (a large subset of Cannings' Exchangeable Models) converge to the Wright-Fisher diffusion, even those with non-Poissonian offspring distributions (e.g., Mohle and Sagitov 2001). E.g., equation (4) in Mohle and Sagitov 2001 shows that in such cases the "coalescent Ne" should be (N-1) / Var(K), essentially matching equation (3) in the present paper.
The criticism of lack of engagement with well-established literature has been responded extensively above. Briefly, the literature is about modifications of the WF model which share the same feature of population sampling. With that feature, the paradoxes are unresolvable. For example, however Ne is defined, the fixation probability of an advantageous mutation does not depend on N or Ne. This is the third paradox of the WF models.
(3) Beyond this, I would imagine that branching processes with heavy-tailed offspring distributions could result in deviations that are not well captured by the authors' WFH model. In this case, the processes are known to converge (backward-in-time) to Lambda or Xi coalescents (e.g., Eldon and Wakely 2006 or again in Mohle and Sagitov 2001 and subsequent papers), which have well-defined forward-in-time processes.
We admire the learned understanding of the literature expressed by the review, which raise two points. First, our model may not be able to handle the heavy-tailed progeny distribution (i.e., the kurtosis of the distribution of k). Second, the Xi coalescence models (cited above) can do that. Below are our clarifications.
First, the WFH model is based on the general distribution of K, which includes flexible and realistic representations of offspring number distributions. In fact, we have used various forms of K distribution in our publications on the evolution of SARS-CoV-2 (see the Ruan et al publications in the bibliography). Power-law distribution is particularly useful as the K-distribution in viral transmission is highly kurtotic. This is reflected in the super-spreader hypothesis. In short, the branching process on which the WFH model is based in is mainly about the distribution of K. Nevertheless, the variance V(K) can often yield good approximations when the kurtosis is modest.
Second, we would like to comment on the models of Eldon and Wakely 2006. or Mohle and Sagitov 2001 and subsequent papers. These papers are based on the Moran model by considering a highly skewed distribution of offspring numbers. Fundamentally, the Moran models generally behave like WF models (standard or modified) and hence have the same problems with the paradoxes that are central to our studies. In fact, the reservations about introducing V(K) into the WF models apply as well to the Moran models. The introduction of V(K) is mathematically valid but biologically untenable. Essentially, the WF models incorporate the Haldane model as a first step in the generation transition. The introduction of V(K) into the Moran model is even less biologically sensible. Furthermore, the model allows K to take only three discrete values: 0, 2, and Nψ (see Eq. (7) in Eldon and Wakely). Their model also assumes a constant population size, which contrasts with our model's flexibility in handling varying population sizes and more complex distributions for K.
In short, the modifications of the WF (and Moran) models are unnecessarily complicated, biologically untenable but still fail to account for the paradoxes. The WFH model can rectify these problems.
(4) These results that Ne in the Wright-Fisher process might not be related to N in any straightforward (or even one-to-one) way are well-known (e.g., Neher and Hallatschek 2012; Spence, Kamm, and Song 2016; Matuszewski, Hildebrandt, Achaz, and Jensen 2018; Rice, Novembre, and Desai 2018; the work of Lounès Chikhi on how Ne can be affected by population structure; etc...)
The reviewer is correct in pointing out the inexact correlation between N and Ne. Nevertheless, it should still be true that the WF models predict qualitatively weaker drift as N increases. The first paradox is as stated:
When the population size (N) is growing exponentially, such as in a bacteria culture, drift is nearly absent when N is small and is much stronger as N increases, especially when approaching the carrying capacity. Such common observations are exactly opposite of the WF model's key prediction.
(5) I was also missing some discussion of the relationship between the branching process and the Wright-Fisher model (or more generally Cannings' Exchangeable Models) when conditioning on the total population size. In particular, if the offspring distribution is Poisson, then conditioned on the total population size, the branching process is identical to the Wright-Fisher model.
We thank the reviewer for this important comment. The main difference is that N is imposed from outside the WF models but can be generated from within the Haldane model (see the density-dependent Haldane model). In nature, N of the next generation is the sum of K’s among members of the population. It is how the Haldane model determines N(t+1) from N(t). In the WF models, N is imposed from outside the model and, hence the given N determines the distribution of K. For this reason, N regulation is not possible in the WF models, thus resulting in the paradoxes.
(6) In the discussion, it is claimed that the last glacial maximum could have caused the bottleneck observed in human populations currently residing outside of Africa. Compelling evidence has been amassed that this bottleneck is due to serial founder events associated with the out-of-Africa migration (see e.g., Henn, Cavalli-Sforza, and Feldman 2012 for an older review - subsequent work has only strengthened this view). For me, a more compelling example of changes in carrying capacity would be the advent of agriculture ~11kya and other more recent technological advances.
We thank the reviewer and have used this more convincing case as suggested by the reviewer.
Recommendations for the authors:
General replies - We thank the editors and reviewers again. The points below are re-iterations of the comments received above and have since been replied in detail. Specific instructions about wording and notations have also been rectified. Again, we are grateful for the inputs from which we learned a great deal.
Reviewing Editor Comments:
The reviewers recognize the value of this model and some of the findings, particularly results from the density-dependent Haldane model. However, they expressed considerable concerns with the model and overall framing of this manuscript.
First, all reviewers pointed out that the manuscript does not sufficiently engage with the extensive literature on various models of effective population size and genetic drift, notably lacking discussion on Cannings models and related works.
We have addressed this issue in the beginning of Introduction and Discussion, pointing to the long section in the new second half of Discussion. The essence is that the literature is all about the modified WF models. The WF-Haldane model is conceptually and operationally distinct from the WF models, either standard or modified ones,
Second, there is a disproportionate discussion on the paradoxes, yet some of the paradoxes might already be resolved within current theoretical frameworks. All three reviewers found the modeling and simulation of the yeast growth experiment hard to follow or lacking justification for certain choices. The analysis approach of sex chromosomes is also questioned.
This criticism is addressed together with the next one as they make the same point.
The reviewers recommend a more thorough review of relevant prior literature to better contextualize their findings. The authors need to clarify and/or modify their derivations and simulations of the yeast growth experiment to address the identified caveats and ensure robustness. Additionally, the empirical analysis of the sex chromosome should be revisited, considering alternative scenarios rather than relying solely on the MSE, which only provides a superficial solution. Furthermore, the manuscript's overall framing should be adjusted to emphasize the conclusions drawn from the WFH model, rather than focusing on the "unresolved paradoxes", as some of these may be more readily explained by existing frameworks. Please see the reviewers' overall assessment and specific comments.
Many thanks. We have carefully reframed and presented the WF-Haldane model to make it clear and logically consistent. Whether a new model (i.e., the WF-Haldane model) deserves to be introduced depends on whether it makes any contribution for understanding nature. That is why we emphasize the four paradoxes.
A most important disagreement between the reviewers and the authors is about the nature of the paradoxes. While the reviewers suggest that they "may" be resolvable by the conventional WF model (standard or modified), they did not offer the possible resolutions. To use the analogy in our provisional response: the WF vs. Haldane models are compared to gas cars vs electric vehicles. We can say confidently that the internal combustion engine cannot resolve the conflicting demands of transportation and zero emission. Its design has limited its capability.
Reviewer #2 (Recommendations For The Authors):
Many thanks. We have incorporated all these suggestions. When the incorporation is not straightforward, we have carefully revised the text to minimize mis-communications.
In the introduction -- "Genetic drift is simply V(K)" -- this is a very strong statement. You can say it is inversely proportional to V(K), but drift is often defined based on changes in allele frequency.
We change the word “simply” to “essentially”. This wording is supported by the fixation probability of advantageous mutations, 2s/(V(k). We have shown in the text that N does not matter here because the fixation is nearly deterministic when the copy number reaches, say, 100, regardless of whether N is 10^4 or 10^8,
Page 3 line 86. "sexes is a sufficient explanation."--> "sex could be a sufficient explanation"
The strongest line of new results is about 2s/V(K). Perhaps, the paper could put more emphasis on this part and demonstrate the generality of this result with a different example.
The math notations in the supplement are not intuitive. e.g., using i_k and j_k as probabilities. I also recommend using E[X] and V[X]for expectation and variance rather than \italic{E(X)} to improve the readability of many equations.
Thank you for your careful reading. Regarding the use of i_k and j_k as probabilities, we initially considered using 𝑝 or 𝑞 to represent probabilities. However, since 𝑝 and 𝑞 are already used in the main text, we opted for 𝑖 and 𝑗 to avoid potential confusion potential confusion. As for your recommendation to use
E[X] and V[X] for expectation and variance, we would like to clarify that we follow the standard practice of italicizing these symbols to represent variables.
Eq A6, A7, While I manage to follow, P_{10}(t) and P_{10} are not defined anywhere in the text.
Supplement page 7, the term "probability of fixation" is confusing in a branching model.Thank you for your observation. We have carefully revised the supplement to provide clarity on these points.
Revision - In population genetics, the fixation of M allele means that the population consist entirely of the M allele, with no W alleles remaining. We define the fixation probability of M allele by generation t as follows:Given that M and W allele reproduce independently, this can be factored as:
As t approaches infinity, the ultimate fixation probability of M allele can be derived as follows:
E.q. A 28. It is unclear eq. A.1 could be used here directly. Some justification would be nice.
We appreciate your careful review, and we will ensure this connection between the two equations is made clearer in the supplement.
Revision - Note we would like to clarify that Eq. (A1) and Eq. (A28) are essentially the same, with the only difference being the subscript 𝑡, which indicates the time dependence in the dynamic process.
Supplement page 17. "the biological meaning of negative..". There is no clear justification for this claim. As a reader, I don't have any intuition as to why that is the case.
Thank you for raising this concern. We have addressed this issue earlier.
-

-

eLife assessment
This study presents a useful modification of a standard model of genetic drift by incorporating variance in offspring numbers, claiming to address several paradoxes in molecular evolution. It is unfortunate that the study fails to engage prior literature that has extensively examined the impact of variance in offspring number, implying that some of the paradoxes presented might be resolved within existing frameworks. In addition, while the modified model yields intriguing theoretical predictions, the simulations and empirical analyses are incomplete to support the authors' claims.
-

Reviewer #1 (Public Review):
Summary:
The authors present a theoretical treatment of what they term the "Wright-Fisher-Haldane" model, a claimed modification of the standard model of genetic drift that accounts for variability in offspring number, and argue that it resolves a number of paradoxes in molecular evolution. Ultimately, I found this manuscript quite strange. The notion of effective population size as inversely related to the variance in offspring number is well known in the literature, and not exclusive to Haldane's branching process treatment. However, I found the authors' point about variance in offspring changing over the course of, e.g. exponential growth fairly interesting, and I'm not sure I'd seen that pointed out before. Nonetheless, I don't think the authors' modeling, simulations, or empirical data analysis are …
Reviewer #1 (Public Review):
Summary:
The authors present a theoretical treatment of what they term the "Wright-Fisher-Haldane" model, a claimed modification of the standard model of genetic drift that accounts for variability in offspring number, and argue that it resolves a number of paradoxes in molecular evolution. Ultimately, I found this manuscript quite strange. The notion of effective population size as inversely related to the variance in offspring number is well known in the literature, and not exclusive to Haldane's branching process treatment. However, I found the authors' point about variance in offspring changing over the course of, e.g. exponential growth fairly interesting, and I'm not sure I'd seen that pointed out before. Nonetheless, I don't think the authors' modeling, simulations, or empirical data analysis are sufficient to justify their claims.
Weaknesses:
I have several outstanding issues. First of all, the authors really do not engage with the literature regarding different notions of an effective population. Most strikingly, the authors don't talk about Cannings models at all, which are a broad class of models with non-Poisson offspring distributions that nonetheless converge to the standard Wright-Fisher diffusion under many circumstances, and to "jumpy" diffusions/coalescents otherwise (see e.g. Mohle 1998, Sagitov (2003), Der et al (2011), etc.). Moreover, there is extensive literature on effective population sizes in populations whose sizes vary with time, such as Sano et al (2004) and Sjodin et al (2005). Of course in many cases here the discussion is under neutrality, but it seems like the authors really need to engage with this literature more.
The most interesting part of the manuscript, I think, is the discussion of the Density Dependent Haldane model (DDH). However, I feel like I did not fully understand some of the derivation presented in this section, which might be my own fault. For instance, I can't tell if Equation 5 is a result or an assumption - when I attempted a naive derivation of Equation 5, I obtained E(K_t) = 1 + r/c*(c-n)*dt. It's unclear where the parameter z comes from, for example. Similarly, is equation 6 a derivation or an assumption? Finally, I'm not 100% sure how to interpret equation 7. I that a variance effective size at time t? Is it possible to obtain something like a coalescent Ne or an expected number of segregating sites or something from this?
Similarly, I don't understand their simulations. I expected that the authors would do individual-based simulations under a stochastic model of logistic growth, and show that you naturally get variance in offspring number that changes over time. But it seems that they simply used their equations 5 and 6 to fix those values. Moreover, I don't understand how they enforce population regulation in their simulations---is N_t random and determined by the (independent) draws from K_t for each individual? In that case, there's no "interaction" between individuals (except abstractly, since logistic growth arises from a model that assumes interactions between individuals). This seems problematic for their model, which is essentially motivated by the fact that early during logistic growth, there are basically no interactions, and later there are, which increases variance in reproduction. But their simulations assume no interactions throughout!
The authors also attempt to show that changing variance in reproductive success occurs naturally during exponential growth using a yeast experiment. However, the authors are not counting the offspring of individual yeast during growth (which I'm sure is quite hard). Instead, they use an equation that estimates the variance in offspring number based on the observed population size, as shown in the section "Estimation of V(K) and E(K) in yeast cells". This is fairly clever, however, I am not sure it is right, because the authors neglect covariance in offspring between individuals. My attempt at this derivation assumes that I_t | I_{t-1} = \sum_{I=1}^{I_{t-1}} K_{i,t-1} where K_{i,t-1} is the number of offspring of individual i at time t-1. Then, for example, E(V(I_t | I_{t-1})) = E(V(\sum_{i=1}^{I_{t-1}} K_{i,t-1})) = E(I_{t-1})V(K_{t-1}) + E(I_{k-1}(I_{k-1}-1))*Cov(K_{i,t-1},K_{j,t-1}). The authors have the first term, but not the second, and I'm not sure the second can be neglected (in fact, I believe it's the second term that's actually important, as early on during growth there is very little covariance because resources aren't constrained, but at carrying capacity, an individual having offspring means that another individuals has to have fewer offspring - this is the whole notion of exchangeability, also neglected in this manuscript). As such, I don't believe that their analysis of the empirical data supports their claim.
Thus, while I think there are some interesting ideas in this manuscript, I believe it has some fundamental issues: first, it fails to engage thoroughly with the literature on a very important topic that has been studied extensively. Second, I do not believe their simulations are appropriate to show what they want to show. And finally, I don't think their empirical analysis shows what they want to show.
References:
Möhle M. Robustness results for the coalescent. Journal of Applied Probability. 1998;35(2):438-447. doi:10.1239/jap/1032192859
Sagitov S. Convergence to the coalescent with simultaneous multiple mergers. Journal of Applied Probability. 2003;40(4):839-854. doi:10.1239/jap/1067436085
Der, Ricky, Charles L. Epstein, and Joshua B. Plotkin. "Generalized population models and the nature of genetic drift." Theoretical population biology 80.2 (2011): 80-99
Sano, Akinori, Akinobu Shimizu, and Masaru Iizuka. "Coalescent process with fluctuating population size and its effective size." Theoretical population biology 65.1 (2004): 39-48
Sjodin, P., et al. "On the meaning and existence of an effective population size." Genetics 169.2 (2005): 1061-1070
-

Reviewer #2 (Public Review):
Summary:
This theoretical paper examines genetic drift in scenarios deviating from the standard Wright-Fisher model. The authors discuss Haldane's branching process model, highlighting that the variance in reproductive success equates to genetic drift. By integrating the Wright-Fisher model with the Haldane model, the authors derive theoretical results that resolve paradoxes related to effective population size.
Strengths:
The most significant and compelling result from this paper is perhaps that the probability of fixing a new beneficial mutation is 2s/V(K). This is an intriguing and potentially generalizable discovery that could be applied to many different study systems.
The authors also made a lot of effort to connect theory with various real-world examples, such as genetic diversity in sex chromosomes …
Reviewer #2 (Public Review):
Summary:
This theoretical paper examines genetic drift in scenarios deviating from the standard Wright-Fisher model. The authors discuss Haldane's branching process model, highlighting that the variance in reproductive success equates to genetic drift. By integrating the Wright-Fisher model with the Haldane model, the authors derive theoretical results that resolve paradoxes related to effective population size.
Strengths:
The most significant and compelling result from this paper is perhaps that the probability of fixing a new beneficial mutation is 2s/V(K). This is an intriguing and potentially generalizable discovery that could be applied to many different study systems.
The authors also made a lot of effort to connect theory with various real-world examples, such as genetic diversity in sex chromosomes and reproductive variance across different species.
Weaknesses:
One way to define effective population size is by the inverse of the coalescent rate. This is where the geometric mean of Ne comes from. If Ne is defined this way, many of the paradoxes mentioned seem to resolve naturally. If we take this approach, one could easily show that a large N population can still have a low coalescent rate depending on the reproduction model. However, the authors did not discuss Ne in light of the coalescent theory. This is surprising given that Eldon and Wakeley's 2006 paper is cited in the introduction, and the multiple mergers coalescent was introduced to explain the discrepancy between census size and effective population size, superspreaders, and reproduction variance - that said, there is no explicit discussion or introduction of the multiple mergers coalescent.
The Wright-Fisher model is often treated as a special case of the Cannings 1974 model, which incorporates the variance in reproductive success. This model should be discussed. It is unclear to me whether the results here have to be explained by the newly introduced WFH model, or could have been explained by the existing Cannings model.
The abstract makes it difficult to discern the main focus of the paper. It spends most of the space introducing "paradoxes".
The standard Wright-Fisher model makes several assumptions, including hermaphroditism, non-overlapping generations, random mating, and no selection. It will be more helpful to clarify which assumptions are being violated in each tested scenario, as V(K) is often not the only assumption being violated. For example, the logistic growth model assumes no cell death at the exponential growth phase, so it also violates the assumption about non-overlapping generations.
The theory and data regarding sex chromosomes do not align. The fact that \hat{alpha'} can be negative does not make sense. The authors claim that a negative \hat{alpha'} is equivalent to infinity, but why is that? It is also unclear how theta is defined. It seems to me that one should take the first principle approach e.g., define theta as pairwise genetic diversity, and start with deriving the expected pair-wise coalescence time under the MMC model, rather than starting with assuming theta = 4Neu. Overall, the theory in this section is not well supported by the data, and the explanation is insufficient.
-

Reviewer #3 (Public Review):
Summary:
Ruan and colleagues consider a branching process model (in their terminology the "Haldane model") and the most basic Wright-Fisher model. They convincingly show that offspring distributions are usually non-Poissonian (as opposed to what's assumed in the Wright-Fisher model), and can depend on short-term ecological dynamics (e.g., variance in offspring number may be smaller during exponential growth). The authors discuss branching processes and the Wright-Fisher model in the context of 3 "paradoxes": (1) how Ne depends on N might depend on population dynamics; (2) how Ne is different on the X chromosome, the Y chromosome, and the autosomes, and these differences do match the expectations base on simple counts of the number of chromosomes in the populations; (3) how genetic drift interacts with …
Reviewer #3 (Public Review):
Summary:
Ruan and colleagues consider a branching process model (in their terminology the "Haldane model") and the most basic Wright-Fisher model. They convincingly show that offspring distributions are usually non-Poissonian (as opposed to what's assumed in the Wright-Fisher model), and can depend on short-term ecological dynamics (e.g., variance in offspring number may be smaller during exponential growth). The authors discuss branching processes and the Wright-Fisher model in the context of 3 "paradoxes": (1) how Ne depends on N might depend on population dynamics; (2) how Ne is different on the X chromosome, the Y chromosome, and the autosomes, and these differences do match the expectations base on simple counts of the number of chromosomes in the populations; (3) how genetic drift interacts with selection. The authors provide some theoretical explanations for the role of variance in the offspring distribution in each of these three paradoxes. They also perform some experiments to directly measure the variance in offspring number, as well as perform some analyses of published data.
Strengths:
(1) The theoretical results are well-described and easy to follow.
(2) The analyses of different variances in offspring number (both experimentally and analyzing public data) are convincing that non-Poissonian offspring distributions are the norm.
(3) The point that this variance can change as the population size (or population dynamics) change is also very interesting and important to keep in mind.
(4) I enjoyed the Density-Dependent Haldane model. It was a nice example of the decoupling of census size and effective size.
Weaknesses:
(1) I am not convinced that these types of effects cannot just be absorbed into some time-varying Ne and still be well-modeled by the Wright-Fisher process.
(2) Along these lines, there is well-established literature showing that a broad class of processes (a large subset of Cannings' Exchangeable Models) converge to the Wright-Fisher diffusion, even those with non-Poissonian offspring distributions (e.g., Mohle and Sagitov 2001). E.g., equation (4) in Mohle and Sagitov 2001 shows that in such cases the "coalescent Ne" should be (N-1) / Var(K), essentially matching equation (3) in the present paper.
(3) Beyond this, I would imagine that branching processes with heavy-tailed offspring distributions could result in deviations that are not well captured by the authors' WFH model. In this case, the processes are known to converge (backward-in-time) to Lambda or Xi coalescents (e.g., Eldon and Wakely 2006 or again in Mohle and Sagitov 2001 and subsequent papers), which have well-defined forward-in-time processes.
(4) These results that Ne in the Wright-Fisher process might not be related to N in any straightforward (or even one-to-one) way are well-known (e.g., Neher and Hallatschek 2012; Spence, Kamm, and Song 2016; Matuszewski, Hildebrandt, Achaz, and Jensen 2018; Rice, Novembre, and Desai 2018; the work of Lounès Chikhi on how Ne can be affected by population structure; etc...)
(5) I was also missing some discussion of the relationship between the branching process and the Wright-Fisher model (or more generally Cannings' Exchangeable Models) when conditioning on the total population size. In particular, if the offspring distribution is Poisson, then conditioned on the total population size, the branching process is identical to the Wright-Fisher model.
(6) In the discussion, it is claimed that the last glacial maximum could have caused the bottleneck observed in human populations currently residing outside of Africa. Compelling evidence has been amassed that this bottleneck is due to serial founder events associated with the out-of-Africa migration (see e.g., Henn, Cavalli-Sforza, and Feldman 2012 for an older review - subsequent work has only strengthened this view). For me, a more compelling example of changes in carrying capacity would be the advent of agriculture ~11kya and other more recent technological advances.
-

Author response:
We thank you for the opportunity to provide a concise response. The criticisms are accurately summarized in the eLife assessment:
the study fails to engage prior literature that has extensively examined the impact of variance in offspring number, implying that some of the paradoxes presented might be resolved within existing frameworks.
The essence of our study is to propose the adoption of the Haldane model of genetic drift, based on the branching process, in lieu of the Wright-Fisher (WF) model, based on sampling, usually binomial. In addition to some extensions of the Haldane model, we present 4 paradoxes that cannot be resolved by the WF model. The reviews suggest that some of the paradoxes could be resolved by the WF model, if we engage prior literature sufficiently.
We certainly could not review all the …
Author response:
We thank you for the opportunity to provide a concise response. The criticisms are accurately summarized in the eLife assessment:
the study fails to engage prior literature that has extensively examined the impact of variance in offspring number, implying that some of the paradoxes presented might be resolved within existing frameworks.
The essence of our study is to propose the adoption of the Haldane model of genetic drift, based on the branching process, in lieu of the Wright-Fisher (WF) model, based on sampling, usually binomial. In addition to some extensions of the Haldane model, we present 4 paradoxes that cannot be resolved by the WF model. The reviews suggest that some of the paradoxes could be resolved by the WF model, if we engage prior literature sufficiently.
We certainly could not review all the literature on genetic drift as there must be thousands of them. Nevertheless, the literature we do not cover is based on the WF model, which has the general properties that all modifications of the WF model share. (We should note that all such modifications share the sampling aspect of the WF model. To model such sampling, N is imposed from outside of the model, rather than self-generating within the model. Most important, these modifications are mathematically valid but biologically untenable, as will be elaborated below. Thus, in concept, the WF and Haldane models are fundamentally different.)
In short, our proposal is general with the key point that the WF model cannot resolve these (and many other) paradoxes. The reviewers disagree (apparently only partially) and we shall be specific in our response below.
We shall first present the 4th paradox, which is about multi-copy gene systems (such as rRNA genes and viruses, see the companion paper). Viruses evolve both within and between hosts. In both stages, there are severe bottlenecks. How does one address the genetic drift in viral evolution? How can we model the effective population sizes both within- and between- hosts? The inability of the WF model in dealing with such multi-copy gene systems may explain the difficulties in accounting for the SARS-CoV-2 evolution. Given the small number of virions transmitted between hosts, drift is strong which we have shown by using the Haldane model (Ruan, Luo, et al. 2021; Ruan, Wen, et al. 2021; Hou, et al. 2023).
As the reviewers suggest, it is possible to modify the WF model to account for some of these paradoxes. However, the modifications are often mathematically convenient but biologically dubious. Much of the debate is about the progeny number, K. (We shall use haploid model for this purpose but diploidy does not pose a problem as stated in the main text.) The modifications relax the constraint of V(k) = E(k) inherent in the WF sampling. One would then ask how V(k) can be different from E(k) in the WF sampling even though it is mathematically feasible (but biologically dubious)? Kimura and Crow (1963) may be the first to offer a biological explanation. If one reads it carefully, Kimura's modification is to make the WF model like the Haldane model. Then, why don't we use the Haldane model in the first place by having two parameters, E(k) and V(k), instead of the one-parameter WF model?
The Haldane model is conceptually simpler. It allows the variation in population size, N, to be generated from within the model, rather than artificially imposed from outside of the model. This brings us to the first paradox, the density-dependent Haldane model. When N is increasing exponentially as in bacterial or yeast cultures, there is almost no drift when N is very low and drift becomes intense as N grows to near the carrying capacity. We do not see how the WF model can resolve this paradox, which can otherwise be resolved by the Haldane model.
The second and third paradoxes are about how much mathematical models of population genetic can be detached from biological mechanisms. The second paradox about sex chromosomes is rooted in the realization of V(k) ≠ E(k). Since E(k) is the same between sexes but V(k) is different, how does the WF sampling give rise to V(k) ≠ E(k)? We are asking a biological question that troubled Kimura and Crow (1963) alluded above. The third paradox is acknowledged by two reviewers. Genetic drift manifested in the fixation probability of an advantageous mutation is 2s/V(k). It is thus strange that the fundamental parameter of drift in the WF model, N (or Ne), is missing. In the Haldane model, drift is determined by V(k) with N being a scaling factor; hence 2s/V(k) makes perfect biological sense,
We now answer the obvious question: If the model is fundamentally about the Haldane model, why do we call it the WF-Haldane model? The reason is that most results obtained by the WF model are pretty good approximations and the branching process may not need to constantly re-derive the results. At least, one can use the WF results to see how well they fit into the Haldane model. In our earlier study (Chen, et al. (2017); Fig. 3), we show that the approximations can be very good in many (or most) settings.
We would like to use the modern analogy of gas-engine cars vs. electric-motor ones. The Haldane model and the WF model are as fundamentally different concepts as the driving mechanisms of gas-powered vs electric cars. The old model is now facing many problems and the fixes are often not possible. Some fixes are so complicated that one starts thinking about simpler solutions. The reservations are that we have invested so much in the old models which might be wasted by the switch. However, we are suggesting the integration of the WF and Haldane models. In this sense, the WF model has had many contributions which the new model gratefully inherits. This is true with the legacy of gas-engine cars inherited by EVs.
The editors also issue the instruction: while the modified model yields intriguing theoretical predictions, the simulations and empirical analyses are incomplete to support the authors' claims.
We are thankful to the editors and reviewers for the thoughtful comments and constructive criticisms. We also appreciate the publishing philosophy of eLife that allows exchanges, debates and improvements, which are the true spirits of science publishing.
References for the provisional author responses
Chen Y, Tong D, Wu CI. 2017. A New Formulation of Random Genetic Drift and Its Application to the Evolution of Cell Populations. Mol. Biol. Evol. 34:2057-2064.
Hou M, Shi J, Gong Z, Wen H, Lan Y, Deng X, Fan Q, Li J, Jiang M, Tang X, et al. 2023. Intra- vs. Interhost Evolution of SARS-CoV-2 Driven by Uncorrelated Selection-The Evolution Thwarted. Mol. Biol. Evol. 40.
Kimura M, Crow JF. 1963. The measurement of effective population number. Evolution:279-288.
Ruan Y, Luo Z, Tang X, Li G, Wen H, He X, Lu X, Lu J, Wu CI. 2021. On the founder effect in COVID-19 outbreaks: how many infected travelers may have started them all? Natl. Sci. Rev. 8:nwaa246.
Ruan Y, Wen H, He X, Wu CI. 2021. A theoretical exploration of the origin and early evolution of a pandemic. Sci Bull (Beijing) 66:1022-1029.
Review comments
eLife assessment
This study presents a useful modification of a standard model of genetic drift by incorporating variance in offspring numbers, claiming to address several paradoxes in molecular evolution.
It is unfortunate that the study fails to engage prior literature that has extensively examined the impact of variance in offspring number, implying that some of the paradoxes presented might be resolved within existing frameworks.
We do not believe that the paradoxes can be resolved.
In addition, while the modified model yields intriguing theoretical predictions, the simulations and empirical analyses are incomplete to support the authors' claims.
Public Reviews:
Reviewer #1 (Public Review):
Summary:
The authors present a theoretical treatment of what they term the "Wright-Fisher-Haldane" model, a claimed modification of the standard model of genetic drift that accounts for variability in offspring number, and argue that it resolves a number of paradoxes in molecular evolution. Ultimately, I found this manuscript quite strange.
The notion of effective population size as inversely related to the variance in offspring number is well known in the literature, and not exclusive to Haldane's branching process treatment. However, I found the authors' point about variance in offspring changing over the course of, e.g. exponential growth fairly interesting, and I'm not sure I'd seen that pointed out before.
Nonetheless, I don't think the authors' modeling, simulations, or empirical data analysis are sufficient to justify their claims.
Weaknesses:
I have several outstanding issues. First of all, the authors really do not engage with the literature regarding different notions of an effective population. Most strikingly, the authors don't talk about Cannings models at all, which are a broad class of models with non-Poisson offspring distributions that nonetheless converge to the standard Wright-Fisher diffusion under many circumstances, and to "jumpy" diffusions/coalescents otherwise (see e.g. Mohle 1998, Sagitov (2003), Der et al (2011), etc.). Moreover, there is extensive literature on effective population sizes in populations whose sizes vary with time, such as Sano et al (2004) and Sjodin et al (2005).
Of course in many cases here the discussion is under neutrality, but it seems like the authors really need to engage with this literature more.
The most interesting part of the manuscript, I think, is the discussion of the Density Dependent Haldane model (DDH). However, I feel like I did not fully understand some of the derivation presented in this section, which might be my own fault. For instance, I can't tell if Equation 5 is a result or an assumption - when I attempted a naive derivation of Equation 5, I obtained E(K_t) = 1 + r/c*(c-n)*dt. It's unclear where the parameter z comes from, for example. Similarly, is equation 6 a derivation or an assumption? Finally, I'm not 100% sure how to interpret equation 7. I that a variance effective size at time t? Is it possible to obtain something like a coalescent Ne or an expected number of segregating sites or something from this?
Similarly, I don't understand their simulations. I expected that the authors would do individual-based simulations under a stochastic model of logistic growth, and show that you naturally get variance in offspring number that changes over time. But it seems that they simply used their equations 5 and 6 to fix those values. Moreover, I don't understand how they enforce population regulation in their simulations---is N_t random and determined by the (independent) draws from K_t for each individual? In that case, there's no "interaction" between individuals (except abstractly, since logistic growth arises from a model that assumes interactions between individuals). This seems problematic for their model, which is essentially motivated by the fact that early during logistic growth, there are basically no interactions, and later there are, which increases variance in reproduction. But their simulations assume no interactions throughout!
The authors also attempt to show that changing variance in reproductive success occurs naturally during exponential growth using a yeast experiment. However, the authors are not counting the offspring of individual yeast during growth (which I'm sure is quite hard). Instead, they use an equation that estimates the variance in offspring number based on the observed population size, as shown in the section "Estimation of V(K) and E(K) in yeast cells". This is fairly clever, however, I am not sure it is right, because the authors neglect covariance in offspring between individuals. My attempt at this derivation assumes that I_t | I_{t-1} = \sum_{I=1}^{I_{t-1}} K_{i,t-1} where K_{i,t-1} is the number of offspring of individual i at time t-1. Then, for example, E(V(I_t | I_{t-1})) = E(V(\sum_{i=1}^{I_{t-1}} K_{i,t-1})) = E(I_{t-1})V(K_{t-1}) + E(I_{k-1}(I_{k-1}-1))*Cov(K_{i,t-1},K_{j,t-1}). The authors have the first term, but not the second, and I'm not sure the second can be neglected (in fact, I believe it's the second term that's actually important, as early on during growth there is very little covariance because resources aren't constrained, but at carrying capacity, an individual having offspring means that another individuals has to have fewer offspring - this is the whole notion of exchangeability, also neglected in this manuscript). As such, I don't believe that their analysis of the empirical data supports their claim.
Thus, while I think there are some interesting ideas in this manuscript, I believe it has some fundamental issues:
first, it fails to engage thoroughly with the literature on a very important topic that has been studied extensively. Second, I do not believe their simulations are appropriate to show what they want to show. And finally, I don't think their empirical analysis shows what they want to show.
References:
Möhle M. Robustness results for the coalescent. Journal of Applied Probability. 1998;35(2):438-447. doi:10.1239/jap/1032192859
Sagitov S. Convergence to the coalescent with simultaneous multiple mergers. Journal of Applied Probability. 2003;40(4):839-854. doi:10.1239/jap/1067436085
Der, Ricky, Charles L. Epstein, and Joshua B. Plotkin. "Generalized population models and the nature of genetic drift." Theoretical population biology 80.2 (2011): 80-99
Sano, Akinori, Akinobu Shimizu, and Masaru Iizuka. "Coalescent process with fluctuating population size and its effective size." Theoretical population biology 65.1 (2004): 39-48
Sjodin, P., et al. "On the meaning and existence of an effective population size." Genetics 169.2 (2005): 1061-1070
Reviewer #2 (Public Review):
Summary:
This theoretical paper examines genetic drift in scenarios deviating from the standard Wright-Fisher model. The authors discuss Haldane's branching process model, highlighting that the variance in reproductive success equates to genetic drift. By integrating the Wright-Fisher model with the Haldane model, the authors derive theoretical results that resolve paradoxes related to effective population size.
Strengths:
The most significant and compelling result from this paper is perhaps that the probability of fixing a new beneficial mutation is 2s/V(K). This is an intriguing and potentially generalizable discovery that could be applied to many different study systems.
The authors also made a lot of effort to connect theory with various real-world examples, such as genetic diversity in sex chromosomes and reproductive variance across different species.
Weaknesses:
One way to define effective population size is by the inverse of the coalescent rate. This is where the geometric mean of Ne comes from. If Ne is defined this way, many of the paradoxes mentioned seem to resolve naturally. If we take this approach, one could easily show that a large N population can still have a low coalescent rate depending on the reproduction model. However, the authors did not discuss Ne in light of the coalescent theory. This is surprising given that Eldon and Wakeley's 2006 paper is cited in the introduction, and the multiple mergers coalescent was introduced to explain the discrepancy between census size and effective population size, superspreaders, and reproduction variance - that said, there is no explicit discussion or introduction of the multiple mergers coalescent.
The Wright-Fisher model is often treated as a special case of the Cannings 1974 model, which incorporates the variance in reproductive success. This model should be discussed. It is unclear to me whether the results here have to be explained by the newly introduced WFH model, or could have been explained by the existing Cannings model.
The abstract makes it difficult to discern the main focus of the paper. It spends most of the space introducing "paradoxes".
The standard Wright-Fisher model makes several assumptions, including hermaphroditism, non-overlapping generations, random mating, and no selection. It will be more helpful to clarify which assumptions are being violated in each tested scenario, as V(K) is often not the only assumption being violated. For example, the logistic growth model assumes no cell death at the exponential growth phase, so it also violates the assumption about non-overlapping generations.
The theory and data regarding sex chromosomes do not align. The fact that \hat{alpha'} can be negative does not make sense. The authors claim that a negative \hat{alpha'} is equivalent to infinity, but why is that? It is also unclear how theta is defined. It seems to me that one should take the first principle approach e.g., define theta as pairwise genetic diversity, and start with deriving the expected pair-wise coalescence time under the MMC model, rather than starting with assuming theta = 4Neu. Overall, the theory in this section is not well supported by the data, and the explanation is insufficient.
{Alpha and alpha' can both be negative. X^2 = 0.47 would yield x = -0.7}
Reviewer #3 (Public Review):
Summary:
Ruan and colleagues consider a branching process model (in their terminology the "Haldane model") and the most basic Wright-Fisher model. They convincingly show that offspring distributions are usually non-Poissonian (as opposed to what's assumed in the Wright-Fisher model), and can depend on short-term ecological dynamics (e.g., variance in offspring number may be smaller during exponential growth). The authors discuss branching processes and the Wright-Fisher model in the context of 3 "paradoxes": (1) how Ne depends on N might depend on population dynamics; (2) how Ne is different on the X chromosome, the Y chromosome, and the autosomes, and these differences do match the expectations base on simple counts of the number of chromosomes in the populations; (3) how genetic drift interacts with selection. The authors provide some theoretical explanations for the role of variance in the offspring distribution in each of these three paradoxes. They also perform some experiments to directly measure the variance in offspring number, as well as perform some analyses of published data.
Strengths:
(1) The theoretical results are well-described and easy to follow.
(2) The analyses of different variances in offspring number (both experimentally and analyzing public data) are convincing that non-Poissonian offspring distributions are the norm.
(3) The point that this variance can change as the population size (or population dynamics) change is also very interesting and important to keep in mind.
(4) I enjoyed the Density-Dependent Haldane model. It was a nice example of the decoupling of census size and effective size.
Weaknesses:
(1) I am not convinced that these types of effects cannot just be absorbed into some time-varying Ne and still be well-modeled by the Wright-Fisher process.
(2) Along these lines, there is well-established literature showing that a broad class of processes (a large subset of Cannings' Exchangeable Models) converge to the Wright-Fisher diffusion, even those with non-Poissonian offspring distributions (e.g., Mohle and Sagitov 2001). E.g., equation (4) in Mohle and Sagitov 2001 shows that in such cases the "coalescent Ne" should be (N-1) / Var(K), essentially matching equation (3) in the present paper.
(3) Beyond this, I would imagine that branching processes with heavy-tailed offspring distributions could result in deviations that are not well captured by the authors' WFH model. In this case, the processes are known to converge (backward-in-time) to Lambda or Xi coalescents (e.g., Eldon and Wakely 2006 or again in Mohle and Sagitov 2001 and subsequent papers), which have well-defined forward-in-time processes.
(4) These results that Ne in the Wright-Fisher process might not be related to N in any straightforward (or even one-to-one) way are well-known (e.g., Neher and Hallatschek 2012; Spence, Kamm, and Song 2016; Matuszewski, Hildebrandt, Achaz, and Jensen 2018; Rice, Novembre, and Desai 2018; the work of Lounès Chikhi on how Ne can be affected by population structure; etc...)
(5) I was also missing some discussion of the relationship between the branching process and the Wright-Fisher model (or more generally Cannings' Exchangeable Models) when conditioning on the total population size. In particular, if the offspring distribution is Poisson, then conditioned on the total population size, the branching process is identical to the Wright-Fisher model.
(6) In the discussion, it is claimed that the last glacial maximum could have caused the bottleneck observed in human populations currently residing outside of Africa. Compelling evidence has been amassed that this bottleneck is due to serial founder events associated with the out-of-Africa migration (see e.g., Henn, Cavalli-Sforza, and Feldman 2012 for an older review - subsequent work has only strengthened this view). For me, a more compelling example of changes in carrying capacity would be the advent of agriculture ~11kya and other more recent technological advances.
Recommendations for the authors:
Reviewing Editor Comments:
The reviewers recognize the value of this model and some of the findings, particularly results from the density-dependent Haldane model. However, they expressed considerable concerns with the model and overall framing of this manuscript.
First, all reviewers pointed out that the manuscript does not sufficiently engage with the extensive literature on various models of effective population size and genetic drift, notably lacking discussion on Cannings models and related works.
Second, there is a disproportionate discussion on the paradoxes, yet some of the paradoxes might already be resolved within current theoretical frameworks. All three reviewers found the modeling and simulation of the yeast growth experiment hard to follow or lacking justification for certain choices. The analysis approach of sex chromosomes is also questioned.
The reviewers recommend a more thorough review of relevant prior literature to better contextualize their findings. The authors need to clarify and/or modify their derivations and simulations of the yeast growth experiment to address the identified caveats and ensure robustness. Additionally, the empirical analysis of the sex chromosome should be revisited, considering alternative scenarios rather than relying solely on the MSE, which only provides a superficial solution. Furthermore, the manuscript's overall framing should be adjusted to emphasize the conclusions drawn from the WFH model, rather than focusing on the "unresolved paradoxes", as some of these may be more readily explained by existing frameworks. Please see the reviewers' overall assessment and specific comments.
Reviewer #2 (Recommendations For The Authors):
In the introduction -- "Genetic drift is simply V(K)" -- this is a very strong statement. You can say it is inversely proportional to V(K), but drift is often defined based on changes in allele frequency.
Page 3 line 86. "sexes is a sufficient explanation."--> "sex could be a sufficient explanation"
The strongest line of new results is about 2s/V(K). Perhaps, the paper could put more emphasis on this part and demonstrate the generality of this result with a different example.
The math notations in the supplement are not intuitive. e.g., using i_k and j_k as probabilities. I also recommend using E[X] and V[X]for expectation and variance rather than \italic{E(X)} to improve the readability of many equations.
Eq A6, A7, While I manage to follow, P_{10}(t) and P_{10} are not defined anywhere in the text.
Supplement page 7, the term "probability of fixation" is confusing in a branching model.
E.q. A 28. It is unclear eq. A.1 could be used here directly. Some justification would be nice.
Supplement page 17. "the biological meaning of negative..". There is no clear justification for this claim. As a reader, I don't have any intuition as to why that is the case.
-