Biological condensates form percolated networks with molecular motion properties distinctly different from dilute solutions
Curation statements for this article:-
Curated by eLife
eLife assessment
The authors report results from experiments and modeling that study the motions of molecules in the dense and dilute phases of biomolecular condensates, with the key finding that molecules in the dense phase of condensates formed by folded domains appear to switch between a confined state with low apparent diffusivity and a mobile state with a high apparent diffusivity that is comparable to that of molecules in the dilute phase. The study provides experimental evidence that is suggestive of phase separation coupled with percolation as the operative mechanism that gives rise to biomolecular condensates.
This article has been Reviewed by the following groups
Discuss this preprint
Start a discussion What are Sciety discussions?Listed in
- Evaluated articles (eLife)
Abstract
Formation of membraneless organelles or biological condensates via phase separation and related processes hugely expands the cellular organelle repertoire. Biological condensates are dense and viscoelastic soft matters instead of canonical dilute solutions. To date, numerous different biological condensates have been discovered, but mechanistic understanding of biological condensates remains scarce. In this study, we developed an adaptive single-molecule imaging method that allows simultaneous tracking of individual molecules and their motion trajectories in both condensed and dilute phases of various biological condensates. The method enables quantitative measurements of concentrations, phase boundary, motion behavior, and speed of molecules in both condensed and dilute phases, as well as the scale and speed of molecular exchanges between the two phases. Notably, molecules in the condensed phase do not undergo uniform Brownian motion, but instead constantly switch between a (class of) confined state(s) and a random diffusion-like motion state. Transient confinement is consistent with strong interactions associated with large molecular networks (i.e., percolation) in the condensed phase. In this way, molecules in biological condensates behave distinctly different from those in dilute solutions. The methods and findings described herein should be generally applicable for deciphering the molecular mechanisms underlying the assembly, dynamics, and consequently functional implications of biological condensates.
Article activity feed
-

-

Author Response
Reviewer #1 (Public Review):
This work by Shen et al. demonstrates a single molecule imaging method that can track the motions of individual protein molecules in dilute and condensed phases of protein solutions in vitro. The authors applied the method to determine the precise locations of individual molecules in 2D condensates, which show heterogeneity inside condensates. Using the time-series data, they could obtain the displacement distributions in both phases, and by assuming a two-state model of trapped and mobile states for the condensed phase, they could extract diffusion behaviors of both states. This approach was then applied to 3D condensate systems, and it was shown that the estimates from the model (i.e., mobile fraction and diffusion coefficients) are useful to quantitatively compare the motions inside …
Author Response
Reviewer #1 (Public Review):
This work by Shen et al. demonstrates a single molecule imaging method that can track the motions of individual protein molecules in dilute and condensed phases of protein solutions in vitro. The authors applied the method to determine the precise locations of individual molecules in 2D condensates, which show heterogeneity inside condensates. Using the time-series data, they could obtain the displacement distributions in both phases, and by assuming a two-state model of trapped and mobile states for the condensed phase, they could extract diffusion behaviors of both states. This approach was then applied to 3D condensate systems, and it was shown that the estimates from the model (i.e., mobile fraction and diffusion coefficients) are useful to quantitatively compare the motions inside condensates. The data can also be used to reconstruct the FRAP curves, which experimentally quantify the mobility of the protein solution.
This work introduces an experimental method to track single molecules in a protein solution and analyzes the data based on a simple model. The simplicity of the model helps a clear understanding of the situation in a test tube, and I think that the model is quite useful in analyzing the condensate behaviors and it will benefit the field greatly. However, the manuscript in its current form fails to situate the work in the right context; many previous works are omitted in this manuscript, exaggerating the novelty of the work. Also, the two- state model is simple and useful, but I am concerned about the limits of the model. They extract the parameters from the experimental data by assuming the model. It is also likely that the molecules have a continuum between fully trapped and fully mobile states, and that this continuum model can also explain the experimental data well.
We thank the reviewer for the warm overview of our work and the insightful comments on the areas that need to be improved. We are very encouraged by the reviewer’s general positive assessment of our approach. We have addressed these comments in the revised manuscript
Reviewer #2 (Public Review):
In this paper, Shen and co-workers report the results of experiments using single particle tracking and FRAP combined with modeling and simulation to study the diffusion of molecules in the dense and dilute phases of various kinds of condensates, including those with strong specific interactions as well as weak specific interactions (IDR-driven). Their central finding is that molecules in the dense phase of condensates with strong specific interactions tend to switch between a confined state with low diffusivity and a mobile state with a diffusivity that is comparable to that of molecules in the dilute phase. In doing so, the study provides experimental evidence for the effect of molecular percolation in biomolecular condensates.
Overall, the experiments are remarkably sophisticated and carefully performed, and the work will certainly be a valuable contribution to the literature. The authors' inquiry into single particle diffusivity is useful for understanding the dynamics and exchange of molecules and how they change when the specific interaction is weak or strong. However, there are several concerns regarding the analysis and interpretation of the results that need to be addressed, and some control experiments that are needed for appropriate interpretation of the results, as detailed further below.
We thank the reviewer for the warm support of our work (assessing that our work is “remarkably sophisticated and carefully performed” and “will certainly be a valuable contribution”) and for the constructive comments/critiques, which we have now addressed in the revised manuscript (please refer to our detailed responses below).
(1) The central finding that the molecules tend to experience transiently confined states in the condensed phase is remarkable and important. This finding is reminiscent of transient "caging"/"trapping" dynamics observed in diverse other crowded and confined systems. Given this, it is very surprising to see the authors interpret the single-molecule motion as being 'normal' diffusion (within the context of a two-state diffusion model), instead of analyzing their data within the context of continuous time random walks or anomalous diffusion, which is generally known to arise from transient trapping in crowded/confined systems. It is not clear that interpreting the results within the context of simple diffusion is appropriate, given their general finding of the two confined and mobile states. Such a process of transient trapping/confinement is known to lead to transient subdiffusion at short times and then diffusive behavior at sufficiently long times. There is a hint of this in the inset of Fig 3, but these data need to be shown on log-log axes to be clearly interpreted. I encourage the authors to think more carefully and critically about the nature of the diffusive model to be used to interpret their results.
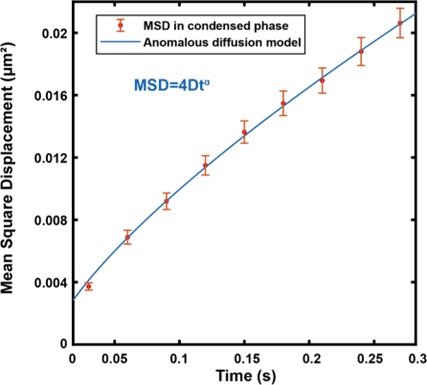
We thank the reviewer for the insightful comments and suggestions, which have been very helpful for us to think deeper about the experimental data and the possible underlying mechanism of our findings. Indeed, the phase separated systems studied here resemble previously studied crowed and confined systems with transient caging/trapping dynamics in the literature ((Akimoto et al., 2011; Bhattacharjee and Datta, 2019; Wong et al., 2004) for examples)(references have been added in the revised manuscript). In our PSD system in Figure 3, The caging/trapping of NR2B in the condensed phase is likely due to its binding to the percolated PSD network. Thus, NR2B molecules in the condensed phase should undergo subdiffusive motions. Indeed, from our single molecule tracking data, the motion of NR2B fits well with the continuous time random walk (CTRW) model, as surmised by this reviewer. We have now fitted the MSD curve of all tracks of NR2B in the condensed phase with an anomalous diffusion model: MSD(t)=4Dtα (see Response Figure 1 below). The fitted α is 0.74±0.03, indicating that NR2B molecules in the condensed phase indeed undergo sub- diffusive motions. The fitted diffusion coefficient D is 0.014±0.001 μm2/s. We have now replaced the Brownian motion fitting in Figure 3E in the original manuscript with this sub- diffusive model fitting in the revised manuscript to highlight the complexity of NR2B diffusion in PSD condensed phase we observed.
Response Figure 1: Fitted the MSD curve (mean value as red dot with standard error as error bar) in condensed phase with an anomalous diffusion model (blue curve, MSD=4Dtα). The fitting gives D=0.014±0.001 μm2/s and α=0.74±0.03.
We find it useful to interpret the apparent diffusion coefficient (D=0.014±0.001 μm2/s) derived from this particular anomalous diffusion model as containing information of NR2B motions in a broadly construed mobile state (i.e., corresponding to the network unbound form) as well as in a broadly construed confined state (i.e., corresponding to NR2B molecules bound to percolated PSD networks). The global fitting using the sub-diffusive model does not pin down motion properties of NR2B in these different motion states. This is why we used, at least as a first approximation, the two-state motion switch model (HMM model) to analyse our data (please refer also to our detailed response to the comment #7 from reviewer 1 and corresponding additional analyses made during the revision as highlighted in Response Figure 4).
As described in our response to the comment points #4 and #7 from reviewer 1, the two- state model is most likely a simplification of NR2B motions in the condensed phase. Both the mobile state and the confined state in our simplified interpretative framework likely represent ensemble averages of their respective motion states. However, the tracking data available currently do not allow us to further distinguish the substates, but further analysis using more refined model in the future may provide more physical insight, as we now emphasize in the revised “Discussion” section: “With this in mind, the two motion states in our simple two-state model for condensed-phase dynamics should be understood to be consisting of multiple sub-states. For instance, one might envision that the percolated molecular network in the condensed phase is not uniform (e.g., existence of locally denser or looser local networks) and dynamic (i.e., local network breaking and forming). Therefore, individual proteins binding to different sub-regions of the network will have different motion properties/states. … In light of this basic understanding, the “confined state” and “mobile state” as well as the derived diffusion coefficients in this work should be understood as reflections of ensemble-averaged properties arising from such an underlying continuum of mobilities. Further development of experimental techniques in conjunction with more refined models of anomalous diffusion (Joo et al., 2020; Kuhn et al., 2021; Muñoz-Gil et al., 2021) will be necessary to characterize these more subtle dynamic properties and to ascertain their physical origins” (p.23 of the revised manuscript).
A practical reason for using the two-state motion switch HMM model to analyse our tracking data in the condensed phase is that the lifetime of the putative mobile state (when the per-frame molecular displacements are relatively large) is very short and such relatively faster short trajectories are interspersed by long confined states (see Response Figure 4C for an example). Statistically, ascertaining a particular anomalous diffusion model by fitting to such short tracks is likely not reliable. Therefore, here we opted for a semi-quantitative interpretative framework by using fitted diffusion coefficients in a two-state HMM as well as the new correlation-based approach for demarcating a low-mobility state and a high- mobility state (see our detailed response to reviewer 1’s point #7) in the present manuscript (which is quite an extensive study already) while leaving refinements of our computational modelling to future effort.
Even in the context of the 'normal' two-state diffusion model they present, if they wish to stick with that-although it seems inappropriate to do so-can the authors provide some physical intuition for what exactly sets the diffusivities they extract from their data. (0.17 and 0.013 microns squared per second for the mobile and confined states). Can these be understood using e.g., the Stoke-Einstein or Ogston models somehow?
As stated above, we are in general agreement with this reviewer that the motion of NR2B in the condensed phase is more complex than the simple two-state picture we adopted as a semi-quantitative interpretation that is adequate for our present purposes. Within the multi-pronged analysis we have performed thus far, NR2B molecules clearly undergo anomalous diffusions in solution containing dense, percolated, and NR2B-binding molecular networks. As a first approximation, our simple two-state HMM analysis yielded two simple diffusion coefficients (0.17 μm2/s for the mobile state and 0.013 μm2/s for the confined state). For the diffusion coefficient in the mobile state, we regard it as providing a time scale for relatively faster diffusive motions (which may be further classified into various motion substates in the future) that are not bound or only weakly associated with the percolated network of strong interactions in the PSD condensed phase. For the confined or low-mobility state in our present formulation, these molecules are likely bound relatively tightly to the percolated networks, thus the diffusion coefficient should be much smaller than the unbounded form (i.e., the mobile state) according to the Stoke-Einstein model. However, due to the detection limitation of the supper resolution imaging method (resolution of ~20 nm), we could not definitively tell the actual diffusivity beyond the resolution limit. So the diffusion coefficient in the confined state can also be interpreted as a Gaussian distributed microscope detection error (𝑓(𝑥) =1
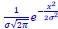 , which is x~N(0, σ2), where σ is the standard deviation of the Gaussian distribution viewed as the resolution of localization-based microscopy, x is the detection error between recorded localization and molecule’s actual position). The track length in the confined state is the distance between localizations in consecutive frames, which can be calculated by subtraction of two independent Gaussian distributions, and the distribution of this track length (r) will be r~N(0, 2σ2). To link the detection error with the fitted diffusion coefficient, we calculated the log likelihood function of Gaussian distributed localization error (
, which is x~N(0, σ2), where σ is the standard deviation of the Gaussian distribution viewed as the resolution of localization-based microscopy, x is the detection error between recorded localization and molecule’s actual position). The track length in the confined state is the distance between localizations in consecutive frames, which can be calculated by subtraction of two independent Gaussian distributions, and the distribution of this track length (r) will be r~N(0, 2σ2). To link the detection error with the fitted diffusion coefficient, we calculated the log likelihood function of Gaussian distributed localization error (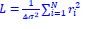 , where σ is the standard deviation of the Gaussian distribution) for the maximum likelihood estimation process to fit the HMM model. The random walk shares a similar log likelihood term (
, where σ is the standard deviation of the Gaussian distribution) for the maximum likelihood estimation process to fit the HMM model. The random walk shares a similar log likelihood term (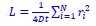 ) in performing maximum likelihood estimation.
) in performing maximum likelihood estimation.These two log likelihood functions will produce same fitting results with 2σ2 equivalent to 4Dt according to the likelihood function. In this way, the diffusion coefficient yielded by our HMM analyses for the confined state (0.0127 μm2/s) can be interpreted as the standard deviation of localization detection error (or microscope resolution limit), which is 𝜎 =√2𝐷𝑡 = 19.5 𝑛𝑚. We have included this consideration as an alternate interpretation of the confined-state or low-mobility motions with the results now provided in the “Materials and Methods” section in the sentence, viz., “… the L-component distribution may be reasonably fitted (albeit with some deviations, see below) to a simple-diffusion functional form with a parameter s =13.6 ± 3.7 nm, where s may be interpreted as a microscope detection error due to imaging limits or alternately expressed as s = DLt with DL = 0.006149 μm2/s being the fitted confined-state diffusion coefficient and t = 0.03s is the time interval of the time step between experimental frames. (The HMM-estimated confined-state Dc = 0.0127 μm2/s corresponds to s = 19.5 nm)” (p.32 of the revised manuscript).
(2) Equation 1 (and hence equation 2) is concerning. Consider a limit when P_m=1, that is, in the condensed phase, there are no confined particles, then the model becomes a diffusion equation with spatially dependent diffusivity, \partial c /\partial t = \nabla * (D(x) \nabla c). The molecules' diffusivity D(x) is D_d in the dilute phase and D_m in the condensed phase. No matter what values D_d and D_m are, at equilibrium the concentration should always be uniform everywhere. According to Equation 1, the concentration ratio will be D_d/D_m, so if D_d/D_m \neq 1, a concentration gradient is generated spontaneously, which violates the second law of thermodynamics. Can the authors please justify the use of this equation?
Indeed, the derivation of Equation 1 appears to be concerning. The flux J is proportional to D
- dc/dx (not kDc as in the manuscript). At equilibrium dc/dx = 0 on both sides and c is constant everywhere. Can the authors please comment?
So then another question is, why does the Monte Carlo simulation result agree with Equation 1? I suspect this has to do with the behavior of particles crossing the boundary. Consider another limit where D_m = 0, that is, particles freeze in the condensed phase. If once a particle enters the condensed phase, it cannot escape, then eventually all particles will end up in the condensed phase and EF=infty. The authors likely used this scheme. But as mentioned above this appears to violate the second law.
Thanks for the incisive comment. After much in-depth considerations, we are in agreement with the reviewer that Eq.1 should not be presented as a relation that is generally applicable to diffusive motions of molecules in all phase-separated systems. There are cases in which this relation can need to unphysical outcomes as correctly pointed out by the reviewer.
Nonetheless, based on our theoretical/computational modeling, it is also clear, empirically, that Eq.1 holds approximately for the NR2B/PSD system we studied, and as such it is a useful approximate relation in our analysis. We have therefore provided a plausible physical perspective for Eq.1’s applicability as an approximate relation based upon a schematic consideration of diffusion on an underlying rugged (free) energy landscape (Zhang and Chan, 2012) of a phase-separated system (See Figure 3G in the revised manuscript), while leaving further studies of such energy landscape models to future investigations.
This additional perspective is now included in the following added passage under a new subheading in the revised manuscript:
"Physical picture and a two-state, two-phase diffusion model for equilibrium and dynamic properties of PSD condensates"
(3) Despite the above two major concerns described in (1) and (2), the enrichment due to the presence of a "confined state", is reasonable. The equilibrium between "confined" and "mobile" states is determined by its interaction with the other proteins and their ratio at equilibrium corresponds to the equilibrium constant. Therefore EF=1/Pm is reasonable and comes solely from thermodynamics. In fact, the equilibrium partition between the dilute and dense phases should solely be a thermodynamic property, and therefore one may expect that it should not have anything to do with diffusivity. Can the authors please comment on this alternative interpretation?
Thanks for this thought-provoking comment. We agree with the reviewer that the relative molecular densities in the condensed versus dilute phases are governed by thermodynamics unless there is energy input into the system. However, in our formulation, the mobile ratio should not be the only parameters for determining the enrichment fold in a phase separated system. In fact, the approximate relation (Eq.1) is EF ≈ Dd/PmDm, and thus EF ≈ 1/Pm only when Dd ≈ Dm . But the speed of mobile-state diffusion in the condensed phase is found to be appreciably smaller than that of diffusion in the dilute phase (Dd > Dm). In general, a hallmark of a phase separation system is to enrich involved molecules in the condensed phase, regardless whether the molecule is a driver (or scaffold) or a client of the system. Such enrichment is expected to be resulted from the net free energy gain due to increased molecular interactions of the condensed phase (as envisioned in Response Figure 9). For example, in the phase separation systems containing PrLD-SAMME (Figure 4 of the manuscript), Pm is close to 1, but the enrichment of PrLD-SAMME in the condensed phase is much greater than 1 (estimated to be ~77, based on the fluorescence intensity of the protein in the dilute and condensed phase; Figure 5—figure supplement 1). As far as Eq.1 is concerned, this is mathematically correct because the diffusion coefficient of PrLD-SAMME in the condensed phase (D ~0.2 μm2/s) is much smaller than the diffusion coefficient of a monomeric molecule with a similar molecular mass in dilute solution (D~ 100 μm2/s, measured by FRAP-based assay; the mobility of the molecules in the dilute solution in 3D is too fast to be tracked). Physically, it’s most likely that the slower molecular motion in the condensed phase is caused by favorable intermolecular interactions and the same favorable interactions underpinning the dynamic effects lead also to a larger equilibrium Boltzmann population.
-

eLife assessment
The authors report results from experiments and modeling that study the motions of molecules in the dense and dilute phases of biomolecular condensates, with the key finding that molecules in the dense phase of condensates formed by folded domains appear to switch between a confined state with low apparent diffusivity and a mobile state with a high apparent diffusivity that is comparable to that of molecules in the dilute phase. The study provides experimental evidence that is suggestive of phase separation coupled with percolation as the operative mechanism that gives rise to biomolecular condensates.
-

Reviewer #1 (Public Review):
This work by Shen et al. demonstrates a single molecule imaging method that can track the motions of individual protein molecules in dilute and condensed phases of protein solutions in vitro. The authors applied the method to determine the precise locations of individual molecules in 2D condensates, which show heterogeneity inside condensates. Using the time-series data, they could obtain the displacement distributions in both phases, and by assuming a two-state model of trapped and mobile states for the condensed phase, they could extract diffusion behaviors of both states. This approach was then applied to 3D condensate systems, and it was shown that the estimates from the model (i.e., mobile fraction and diffusion coefficients) are useful to quantitatively compare the motions inside condensates. The data …
Reviewer #1 (Public Review):
This work by Shen et al. demonstrates a single molecule imaging method that can track the motions of individual protein molecules in dilute and condensed phases of protein solutions in vitro. The authors applied the method to determine the precise locations of individual molecules in 2D condensates, which show heterogeneity inside condensates. Using the time-series data, they could obtain the displacement distributions in both phases, and by assuming a two-state model of trapped and mobile states for the condensed phase, they could extract diffusion behaviors of both states. This approach was then applied to 3D condensate systems, and it was shown that the estimates from the model (i.e., mobile fraction and diffusion coefficients) are useful to quantitatively compare the motions inside condensates. The data can also be used to reconstruct the FRAP curves, which experimentally quantify the mobility of the protein solution.
This work introduces an experimental method to track single molecules in a protein solution and analyzes the data based on a simple model. The simplicity of the model helps a clear understanding of the situation in a test tube, and I think that the model is quite useful in analyzing the condensate behaviors and it will benefit the field greatly. However, the manuscript in its current form fails to situate the work in the right context; many previous works are omitted in this manuscript, exaggerating the novelty of the work. Also, the two-state model is simple and useful, but I am concerned about the limits of the model. They extract the parameters from the experimental data by assuming the model. It is also likely that the molecules have a continuum between fully trapped and fully mobile states, and that this continuum model can also explain the experimental data well.
-

Reviewer #2 (Public Review):
In this paper, Shen and co-workers report the results of experiments using single particle tracking and FRAP combined with modeling and simulation to study the diffusion of molecules in the dense and dilute phases of various kinds of condensates, including those with strong specific interactions as well as weak specific interactions (IDR-driven). Their central finding is that molecules in the dense phase of condensates with strong specific interactions tend to switch between a confined state with low diffusivity and a mobile state with a diffusivity that is comparable to that of molecules in the dilute phase. In doing so, the study provides experimental evidence for the effect of molecular percolation in biomolecular condensates.
Overall, the experiments are remarkably sophisticated and carefully performed, …
Reviewer #2 (Public Review):
In this paper, Shen and co-workers report the results of experiments using single particle tracking and FRAP combined with modeling and simulation to study the diffusion of molecules in the dense and dilute phases of various kinds of condensates, including those with strong specific interactions as well as weak specific interactions (IDR-driven). Their central finding is that molecules in the dense phase of condensates with strong specific interactions tend to switch between a confined state with low diffusivity and a mobile state with a diffusivity that is comparable to that of molecules in the dilute phase. In doing so, the study provides experimental evidence for the effect of molecular percolation in biomolecular condensates.
Overall, the experiments are remarkably sophisticated and carefully performed, and the work will certainly be a valuable contribution to the literature. The authors' inquiry into single particle diffusivity is useful for understanding the dynamics and exchange of molecules and how they change when the specific interaction is weak or strong. However, there are several concerns regarding the analysis and interpretation of the results that need to be addressed, and some control experiments that are needed for appropriate interpretation of the results, as detailed further below.
(1) The central finding that the molecules tend to experience transiently confined states in the condensed phase is remarkable and important. This finding is reminiscent of transient "caging"/"trapping" dynamics observed in diverse other crowded and confined systems. Given this, it is very surprising to see the authors interpret the single-molecule motion as being 'normal' diffusion (within the context of a two-state diffusion model), instead of analyzing their data within the context of continuous time random walks or anomalous diffusion, which is generally known to arise from transient trapping in crowded/confined systems. It is not clear that interpreting the results within the context of simple diffusion is appropriate, given their general finding of the two confined and mobile states. Such a process of transient trapping/confinement is known to lead to transient subdiffusion at short times and then diffusive behavior at sufficiently long times. There is a hint of this in the inset of Fig 3, but these data need to be shown on log-log axes to be clearly interpreted. I encourage the authors to think more carefully and critically about the nature of the diffusive model to be used to interpret their results.
Even in the context of the 'normal' two-state diffusion model they present, if they wish to stick with that-although it seems inappropriate to do so-can the authors provide some physical intuition for what exactly sets the diffusivities they extract from their data. (0.17 and 0.013 microns squared per second for the mobile and confined states). Can these be understood using e.g., the Stoke-Einstein or Ogston models somehow?
(2) Equation 1 (and hence equation 2) is concerning. Consider a limit when P_m=1, that is, in the condensed phase, there are no confined particles, then the model becomes a diffusion equation with spatially dependent diffusivity, \partial c /\partial t = \nabla * (D(x) \nabla c). The molecules' diffusivity D(x) is D_d in the dilute phase and D_m in the condensed phase. No matter what values D_d and D_m are, at equilibrium the concentration should always be uniform everywhere. According to Equation 1, the concentration ratio will be D_d/D_m, so if D_d/D_m \neq 1, a concentration gradient is generated spontaneously, which violates the second law of thermodynamics. Can the authors please justify the use of this equation?
Indeed, the derivation of Equation 1 appears to be concerning. The flux J is proportional to D * dc/dx (not k*D*c as in the manuscript). At equilibrium dc/dx = 0 on both sides and c is constant everywhere. Can the authors please comment?
So then another question is, why does the Monte Carlo simulation result agree with Equation 1? I suspect this has to do with the behavior of particles crossing the boundary. Consider another limit where D_m = 0, that is, particles freeze in the condensed phase. If once a particle enters the condensed phase, it cannot escape, then eventually all particles will end up in the condensed phase and EF=infty. The authors likely used this scheme. But as mentioned above this appears to violate the second law.
(3) Despite the above two major concerns described in (1) and (2), the enrichment due to the presence of a "confined state", is reasonable. The equilibrium between "confined" and "mobile" states is determined by its interaction with the other proteins and their ratio at equilibrium corresponds to the equilibrium constant. Therefore EF=1/P_m is reasonable and comes solely from thermodynamics. In fact, the equilibrium partition between the dilute and dense phases should solely be a thermodynamic property, and therefore one may expect that it should not have anything to do with diffusivity. Can the authors please comment on this alternative interpretation?
-