Information transfer in mammalian glycan-based communication

Article activity feed

1. 

   Version published to 10.7554/elife.69415 on eLife

   Feb 20, 2023
2. 

   eLife

   Oct 20, 2022

   Author Response

   Reviewer #1 (Public Review):

   This manuscript applies the framework of information theory to study a subset of cellular receptors (called lectins) that bind to glycan molecules, with a specific focus on the kinds of glycans that are typical of fungal pathogens. The authors use the concentration of various types of ligands as the input to the signaling channel, and measure the "response" of individual cells using a GFP reporter whose expression is driven by a promoter that responds to NFκB. While this work is overall technically solid, I would suggest that readers keep several issues in mind while evaluating these results.

   1. One of the largest potential limitations of the study is the reliance of the authors on exogenous expression of the relevant receptors in U937 cells. Using a cell-line system like this has several …

   Author Response

   Reviewer #1 (Public Review):

   This manuscript applies the framework of information theory to study a subset of cellular receptors (called lectins) that bind to glycan molecules, with a specific focus on the kinds of glycans that are typical of fungal pathogens. The authors use the concentration of various types of ligands as the input to the signaling channel, and measure the "response" of individual cells using a GFP reporter whose expression is driven by a promoter that responds to NFκB. While this work is overall technically solid, I would suggest that readers keep several issues in mind while evaluating these results.

   1. One of the largest potential limitations of the study is the reliance of the authors on exogenous expression of the relevant receptors in U937 cells. Using a cell-line system like this has several advantages, most notably the fact that the authors can engineer different reporters and different combinations of receptors easily into the same cells. This would be much more difficult with, say, primary cells extracted from a mouse or a human. While the ability to introduce different proteins into the cells is a benefit, the problem is that it is not clear how physiologically relevant the results are. To their credit, the authors perform several controls that suggest that differences in transfection efficiency are not the source of the differences in channel capacity between, say, dectin-1 and dectin-2. As the authors themselves clearly demonstrate, however, the differences in the properties of these signaling system are not based on receptor expression levels, but rather on some other property of the receptor. Now, it could be that the dectin-2 receptor is somehow just more "noisy" in terms of its activity compared to, say, dectin-1. This seems a somewhat less likely explanation, however, and so it is likely that downstream details of the signaling systems differ in some way between dectin-2 and the more "information efficient" receptors studied by the authors.

   The channel capacity of a cell signaling network depends critically on the distributions of the downstream signaling molecules in question: see the original paper by Cheong et al. (2011, Science 334 (6054), 354-8) and subsequent papers (notably Selimkhanov et al. (2014) Science 346 (6215), 1370-3 and Suderman et al. (2018) Interface Focus 8 (6), 20180039). The U937 cells considered here clearly don't serve the physiological function of detecting the glycans considered by the authors; despite the fact that this is an artificial cell line, the fact the authors have to exogenously express the relevant receptors indicates that these cells are not necessarily a good model for the types of cells in the body that actually have evolved to sense these glycan molecules.

   Signaling molecules readily exhibit cell-type-specific expression levels that influence cellular responses to external stimuli (Rowland et al.(2017) Nat Commun 8, 16009). So it is unclear that the distributions of downstream signaling molecules in U937 cells mirror those that would be observed in the immune cell types relevant to this response. As such, the physiological relevance of the differences between dectin-2 channel capacities and those exhibited by the other receptors are currently unclear.

   We appreciate Reviewer #1’s in-depth comments related to physiological relevance of the U937 cell. A big benefit of using information theory to investigate a biological communication channel is the realization of quantitative measurement of information that the channel transmits without having detailed measurement of spatiotemporal dynamics of receptors and downstream signaling cascades. In addition, the quantity of measured information itself in turn gives us a decent prediction about detailed signaling mechanisms by comparing the information quantity difference. For example, we investigated how transmission of glycan information from dectin-2 is synergistically modulated in the presence of either dectin-1, DC-SIGN or mincle. Our approach allows to investigate how individual lectins on immune cells contribute to glycan information transmission and be integrated in the presence other type of lectins. Therefore, the findings describe how physiologically relevant lectins are integrating the extracellular signal in a more defined way. Furthermore, we found that our model cell line has one order of magnitude higher expression of dectin-2 compared with primary human monocytes and exhibits a similar zymosan binding pattern (will be described in Recommendations for the authors and Figure R8).

   We fully agree that acquiring more information on the information transmission capability of primary immune cells would increase physiological relevance. In the revised manuscript we addressed this concern by comparing the receptor expression levels of our model cell lines with primary monocytes, for which we find an agreement of cellular heterogeneity. However, we would also like to point out that the very basic nature of our question, of how information stored in glycans is processed by lectins, is not tightly bound to these difference of primary cells and cell lines.

   Line 382: Finally, it is important to take into consideration that our conclusions came from model cell lines, which were used as a surrogate for cell-type-specific lectin expression patterns of primary immune cells. Human monocytes and dectin-2 positive U937 cells have comparable receptor densities and respond similar to stimulation with zymosan particles (SI Fig. 6A and B).

   1. Another issue that readers might want to keep in mind is that the details of the channel capacity calculation are a bit unclear as the manuscript is currently written. The authors indicate that their channel capacity calculations follow the approach of Cheong et al. (2011) Science 334 (6054), 354-8. However, the extent to which they follow that previous approach is not obvious. For instance, the calculations presented in the 2011 work use a combined bootstrapping/linear extrapolation approach to estimate the mutual information at infinite population size in order to deal with known inaccuracies in the calculation that arise from finite-size effects. The Cheong approach also deals with the question of how many bins to use in order to estimate the joint probability distribution across signal and response.

   They do this by comparing the mutual information they calculate for the real data with that calculated for random data to ensure that they are not calculating spuriously high mutual information based on having too many bins. While the Cheong et al. paper does a great job explaining why these steps need to be undertaken, a subsequent paper by Suderman et al. (2017, PNAS 114 (22), 5755-60) explains the approach in even greater detail in the supporting information. Those authors also implemented several improvements to the general approach, including a bootstrap method for more accurately estimating the error in the mutual information and channel capacity estimates.

   The problem here is that, while the authors claim to follow the approach of Cheong et al., it seems that they have re-implemented the calculation, and they do not provide sufficient detail to evaluate the extent to which they are performing the same exact calculation. Since estimates of mutual information are technically challenging, specific details of the steps in their approach would be helpful in order to understand how closely their results can be compared with the results of previous authors. For instance, Cheong et al. estimate the "channel capacity" by trying a set of likely unimodal and bimodal distributions for the input to the channel, and choosing the maximal value as the channel capacity. This is clearly a very approximate approach, since the channel capacity is defined as the supremum over an (uncountably infinite) set of input probability distributions. In any case, the authors of the current manuscript use a different approach to this maximization problem. Although it is a bit unclear how their approach works, it seems that they treat the probability of each input bin as an independent parameter (under the constraint that the probabilities sum to one) and then use an optimization algorithm implemented in Python to maximize the mutual information. In principle, this could be a better approach, since the set of input distributions considered is potentially much larger. The details of the optimization algorithm matter, however, and those are currently unclear as the paper is written.

   We thank Reviewer #1’s recommendation for increasing the legitimacy of the calculation. In the revised manuscript we tried to explain channel capacity calculation procedures in more detail with statistical approaches that adopted from Cheong et al. (2011) and Suderman et al. (2018) (SI section 1 and 2). Furthermore, we decide the number of binning from not only random dataset but also the number of total samples as shown below:

   

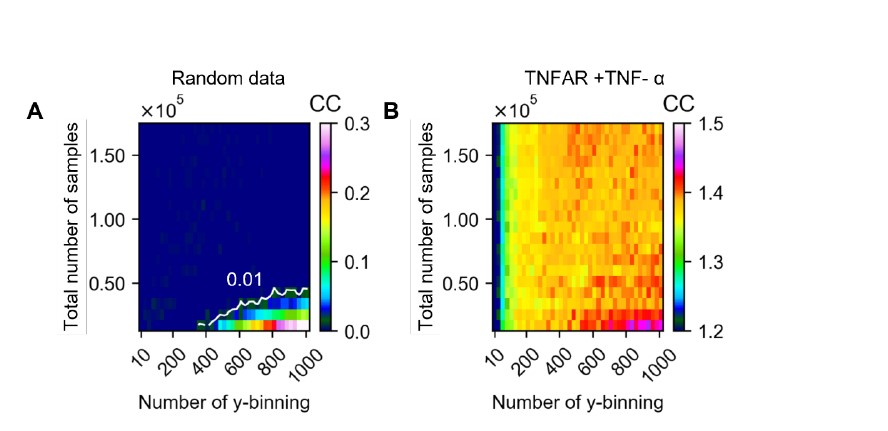
   Figure R1. A) Extrapolated channel capacity values of random dataset at infinitely subsampled distribution under various total number of samples and output binning. The white line in the heatmap represents the channel capacity value at 0.01 bit. B) Extrapolated channel capacity values at infinite subsample size of U937 cells’ input (TNF-a doses) and output (GFP reporter) response.

   Figure R1 describes channel capacity values from random (A) and experimental dataset (B, TNFAR + TNF-a). The channel capacity values from random data indicates the dependence of channel capacity on the number of the output binning and total number sample. According to this heatmap, we decided the allowed bias as 0.01 bits as shown in contour line shown in Figure R1A. Since our minimum dataset that used for channel capacity calculation in the absence of labelled input is near 90,000, the expected bias in channel capacity calculation is therefore less than 0.01 bits in binning range from 10 to 1000 as shown in Figure R1A.

   Furthermore, we demonstrated mutual information maximization procedure using predefined unibimodal input distribution and compared with the systematic method that we used in the work. We found that there is no noticeable difference in channel capacity value between two approaches (SI Figure 3M).

   1. Another issue to be careful about when interpreting these findings is the fact that the authors use logarithmic bins when calculating the channel capacity estimates. This is equivalent to saying that the "output" of the cell signaling channel is not the amount of protein produced under the control of the NFκB promoter, but rather the log of the protein level. Essentially, the authors are considering a case where the relevant output of the system is not the amount of protein itself, but the fold change in the amount of protein. That might be a reasonable assumption, especially if the protein being produced is a transcription factor whose own promoters have evolved to detect fold changes. For many proteins, however, the cell is likely responsive to linear changes in protein concentration, not fold changes. And so choosing the log of the protein level as the output may not make sense in terms of understanding how much information is actually contained in this particular output variable. Regardless, choosing logarithmic bins is not purely a matter of convenience or arbitrary choice, but rather corresponds to a very strong statement about what the relevant output of the channel is.

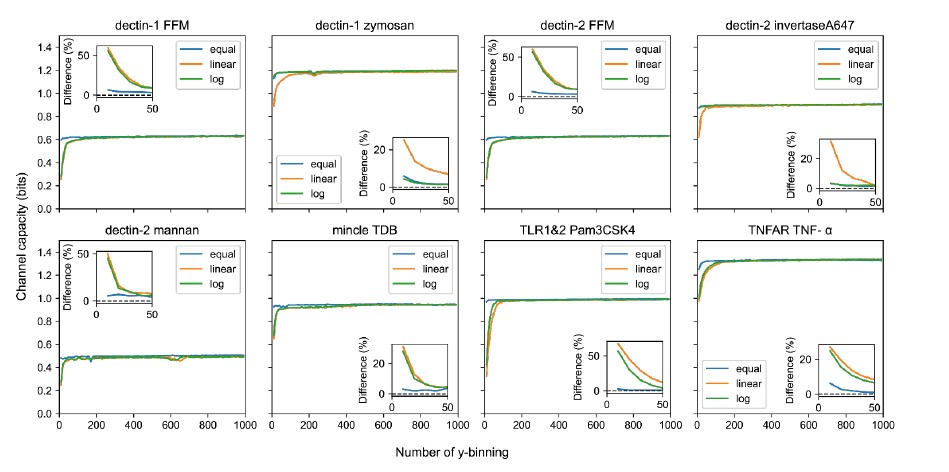
   We understand Reviewer #1’s concern regarding the choice of log binning. We found that if the number of binning is higher than 200, no matter the binning methods, including linear, logarithmic or equal frequency, the estimated channel capacities in each binning number are converged into the same value. The only difference is how quickly the values approach the converged channel capacity as increasing the binning number (shown in Figure R2). In the revised manuscript, we used linear binning to represent more relevant protein signaling as the Reviewer mentioned. Note that the channel capacity values calculated from linear binning do not show noticeable different from our previously calculated channel capacity values.

   On the other hand, linear binning generates significant bias, if we consider labelled input (i.e., continuous input) into channel capacity calculation, due to the increase of binning in input region.

   

   Figure R2. Output binning number and binning method dependence of channel capacity value for experimental dataset. The inset plots show the relative difference of channel capacity value to the maximum channel capacity value in the entire binning range (i.e., from 10 to 1000) of the corresponding binning method.

   According to Reviewer #1’s comment we have changed the binning method from logarithmic binning to linear binning in the whole experimental dataset except in the presence of labelled input (i.e., dectin-2 antibody). If we consider channel capacity between labelled input and NF-kB reporter, equal frequency binning is used for every layer of the channel capacity (i.e., labelled input-binding, binding-GFP, labelled input-GFP)

   Reviewer #2 (Public Review):

   My expertise is more on the theoretical than the experimental aspects of this paper, so those will be the focus of these comments.

   Signal transduction is an important area of study for mathematical biologists and biophysicists. This setting is a natural one for information-theoretic methods, and such methods are attracting increasing research interest. Experimental results that attempt to directly quantify the Shannon capacity of signal transduction are particularly interesting. This paper represents an important contribution to this emerging field.

   My main comments are about the rigorousness and correctness of the theoretical results. More details about these results would improve the paper and help the reader understand the results.

   We understand reviewer #2’s comment related with rigorousness and correctness of the theoretical results of this work. In the revised manuscript, we added following contents to help the reader to better understand the channel capacity calculation procedures.

   • General illustrative introduction regarding how we measured input and output dataset and how we handle those data to prepare joint probability distribution shown in SI section 1.1 and 1.2.

   • Exemplified mutual information maximization procedure using experimental and arbitrary dataset shown in SI section 1.3.

   The calculation of channel capacity, given in the methods, is quite a standard calculation and appears to be correct. However, I was confused by the use of the "weighting value" w_i, which is not specified in the manuscript. The input distribution appears to be a product of the weight w_i and the input probability value p_i, and these appear always to occur together as a product w_i p_i. (In joint probabilities w_i p(i,j), the input probability can be extracted using Bayes' rule, leaving w_i p_i p(j|i).) This leads met wonder two things. First, what role does w_i play (is it even necessary)? Second, of particular interest here is the capacity-achieving input distribution p_i, but w_i obscures it; is the physical input distribution p_i equal to the capacity-achieving distribution? If not, what is the meaning of capacity?

   We thank Reviewer #2’s comment regarding the arbitrariness of the weightings. We realize there was a lack of explanation on the weighting values in the original manuscript. 𝑃x(𝑖) is a marginal probability distribution of input from the original dataset and 𝑃x'(𝑖) is the marginal probability distribution of modified input that maximize the mutual information. In usual case 𝑃x(𝑖) is not equal to 𝑃x'(𝑖) and therefore one needs to find 𝑃x'(𝑖) from 𝑃x(𝑖). Because 𝑃x'(𝑖) is a linear combination of 𝑃x(𝑖), it can be expressed as 𝑤(𝑖)𝑃x(𝑖) , where 𝑤(𝑖) is the weightings, under constraint ∑input/i 𝑤(𝑖)𝑃x (𝑖) = 1 . The changed input distribution, in turn, modifies the joint probability distribution as 𝑃'xy (𝑖, 𝑗) = 𝑤(𝑖)𝑃xy)(𝑖, 𝑗). To help readers understand of this work we expanded the Appendix with illustrative descriptions.

   A more minor but important point: the inputs and outputs of the communication channel are never explicitly defined, which makes the meaning of the results unclear. When evaluating the capacity of an information channel, the inputs X and outputs Y should be carefully defined, so that the mutual information I(X;Y) is meaningful; the mutual information is then maximized to obtain capacity. Although it can be inferred that the input X is the ligand concentration, and the output Y is the expression of GFP, it would be helpful if this were stated explicitly.

   We agree with Reviewer’s suggestion for better description of input and output in the manuscript. Therefore, we have modified Figure 1 A and B and the main text to describe the source of input and output much clearly, as follows:

   Line 92: Accounting for the stochastic behavior of cellular signaling, information theory provides robust and quantitative tools to analyze complex communication channels. A fundamental metric of information theory is entropy, which determines the amount of disorder or uncertainty of variables. In this respect, cellular signaling pathways having high variability of the initiating input signals (e.g. stimulants) and the corresponding highly variable output response (i.e. cellular signaling) can be characterized as a high entropy. Importantly, input and output can have mutual dependence and therefore knowing the input distribution can partly provide the information of output distribution. If noise is present in the communication channel, input and output have reduced mutual dependence. This mutual dependence between input and output is called mutual information. Mutual information is, therefore, a function of input distribution and the upper bound of mutual information is called channel capacity (SI section 1) (Cover and Thomas, 2012). In this report, a communication channel describes signal transduction pathway of C-type lectin receptor, which ultimately lead to NF-κB translocation and finally GFP expression in the reporter model (Fig. 1A). To quantify the signaling information of the communication channels, we used channel capacity. Importantly, the channel capacity isn’t merely describing the resulting maximum intensity of the reporter cells. The channel capacity takes cellular variation and activation across a whole range of incoming stimulus of single cell resolved data into account and quantifies all of that data into a single number.

   Read the original source
3. 

   eLife

   Aug 27, 2021

   Evaluation Summary:

   This manuscript applies the framework of information theory to lectin-glycan signaling modulating the NF-kappaB response. The paper suggests that the information transfer capacity and information flow through the signaling pathway may be affected by a combined action of two distinct receptors having different distributions across a cell population, with possible implications for the immune response. The paper can have an impact on our understanding of signaling through multiple receptors converging on the same output, and will be of interest to experts in cellular signaling, particularly those with interest in innate immune response.

   (This preprint has been reviewed by eLife. We include the public reviews from the reviewers here; the authors also receive private feedback with suggested changes to the manuscript. The …

   Evaluation Summary:

   This manuscript applies the framework of information theory to lectin-glycan signaling modulating the NF-kappaB response. The paper suggests that the information transfer capacity and information flow through the signaling pathway may be affected by a combined action of two distinct receptors having different distributions across a cell population, with possible implications for the immune response. The paper can have an impact on our understanding of signaling through multiple receptors converging on the same output, and will be of interest to experts in cellular signaling, particularly those with interest in innate immune response.

   (This preprint has been reviewed by eLife. We include the public reviews from the reviewers here; the authors also receive private feedback with suggested changes to the manuscript. The reviewers remained anonymous to the authors.)

   Read the original source
4. 

   eLife

   Aug 27, 2021

   Reviewer #1 (Public Review):

   This manuscript applies the framework of information theory to study a subset of cellular receptors (called lectins) that bind to glycan molecules, with a specific focus on the kinds of glycans that are typical of fungal pathogens. The authors use the concentration of various types of ligands as the input to the signaling channel, and measure the "response" of individual cells using a GFP reporter whose expression is driven by a promoter that responds to NFκB. While this work is overall technically solid, I would suggest that readers keep several issues in mind while evaluating these results.

   1. One of the largest potential limitations of the study is the reliance of the authors on exogenous expression of the relevant receptors in U937 cells. Using a cell-line system like this has several advantages, most …

   Reviewer #1 (Public Review):

   This manuscript applies the framework of information theory to study a subset of cellular receptors (called lectins) that bind to glycan molecules, with a specific focus on the kinds of glycans that are typical of fungal pathogens. The authors use the concentration of various types of ligands as the input to the signaling channel, and measure the "response" of individual cells using a GFP reporter whose expression is driven by a promoter that responds to NFκB. While this work is overall technically solid, I would suggest that readers keep several issues in mind while evaluating these results.

   1. One of the largest potential limitations of the study is the reliance of the authors on exogenous expression of the relevant receptors in U937 cells. Using a cell-line system like this has several advantages, most notably the fact that the authors can engineer different reporters and different combinations of receptors easily into the same cells. This would be much more difficult with, say, primary cells extracted from a mouse or a human. While the ability to introduce different proteins into the cells is a benefit, the problem is that it is not clear how physiologically relevant the results are. To their credit, the authors perform several controls that suggest that differences in transfection efficiency are not the source of the differences in channel capacity between, say, dectin-1 and dectin-2. As the authors themselves clearly demonstrate, however, the differences in the properties of these signaling system are not based on receptor expression levels, but rather on some other property of the receptor. Now, it could be that the dectin-2 receptor is somehow just more "noisy" in terms of its activity compared to, say, dectin-1. This seems a somewhat less likely explanation, however, and so it is likely that downstream details of the signaling systems differ in some way between dectin-2 and the more "information efficient" receptors studied by the authors.

   The channel capacity of a cell signaling network depends critically on the distributions of the downstream signaling molecules in question: see the original paper by Cheong et al. (2011, Science 334 (6054), 354-8) and subsequent papers (notably Selimkhanov et al. (2014) Science 346 (6215), 1370-3 and Suderman et al. (2018) Interface Focus 8 (6), 20180039). The U937 cells considered here clearly don't serve the physiological function of detecting the glycans considered by the authors; despite the fact that this is an artificial cell line, the fact the authors have to exogenously express the relevant receptors indicates that these cells are not necessarily a good model for the types of cells in the body that actually have evolved to sense these glycan molecules. Signaling molecules readily exhibit cell-type-specific expression levels that influence cellular responses to external stimuli (Rowland et al. (2017) Nat Commun 8, 16009). So it is unclear that the distributions of downstream signaling molecules in U937 cells mirror those that would be observed in the immune cell types relevant to this response. As such, the physiological relevance of the differences between dectin-2 channel capacities and those exhibited by the other receptors are currently unclear.

   1. Another issue that readers might want to keep in mind is that the details of the channel capacity calculation are a bit unclear as the manuscript is currently written. The authors indicate that their channel capacity calculations follow the approach of Cheong et al. (2011) Science 334 (6054), 354-8. However, the extent to which they follow that previous approach is not obvious. For instance, the calculations presented in the 2011 work use a combined bootstrapping/linear extrapolation approach to estimate the mutual information at infinite population size in order to deal with known inaccuracies in the calculation that arise from finite-size effects. The Cheong approach also deals with the question of how many bins to use in order to estimate the joint probability distribution across signal and response. They do this by comparing the mutual information they calculate for the real data with that calculated for random data to ensure that they are not calculating spuriously high mutual information based on having too many bins. While the Cheong et al. paper does a great job explaining why these steps need to be undertaken, a subsequent paper by Suderman et al. (2017, PNAS 114 (22), 5755-60) explains the approach in even greater detail in the supporting information. Those authors also implemented several improvements to the general approach, including a bootstrap method for more accurately estimating the error in the mutual information and channel capacity estimates.

   The problem here is that, while the authors claim to follow the approach of Cheong et al., it seems that they have re-implemented the calculation, and they do not provide sufficient detail to evaluate the extent to which they are performing the same exact calculation. Since estimates of mutual information are technically challenging, specific details of the steps in their approach would be helpful in order to understand how closely their results can be compared with the results of previous authors. For instance, Cheong et al. estimate the "channel capacity" by trying a set of likely unimodal and bimodal distributions for the input to the channel, and choosing the maximal value as the channel capacity. This is clearly a very approximate approach, since the channel capacity is defined as the supremum over an (uncountably infinite) set of input probability distributions. In any case, the authors of the current manuscript use a different approach to this maximization problem. Although it is a bit unclear how their approach works, it seems that they treat the probability of each input bin as an independent parameter (under the constraint that the probabilities sum to one) and then use an optimization algorithm implemented in Python to maximize the mutual information. In principle, this could be a better approach, since the set of input distributions considered is potentially much larger. The details of the optimization algorithm matter, however, and those are currently unclear as the paper is written.

   1. Another issue to be careful about when interpreting these findings is the fact that the authors use logarithmic bins when calculating the channel capacity estimates. This is equivalent to saying that the "output" of the cell signaling channel is not the amount of protein produced under the control of the NFκB promoter, but rather the log of the protein level. Essentially, the authors are considering a case where the relevant output of the system is not the amount of protein itself, but the fold change in the amount of protein. That might be a reasonable assumption, especially if the protein being produced is a transcription factor whose own promoters have evolved to detect fold changes. For many proteins, however, the cell is likely responsive to linear changes in protein concentration, not fold changes. And so choosing the log of the protein level as the output may not make sense in terms of understanding how much information is actually contained in this particular output variable. Regardless, choosing logarithmic bins is not purely a matter of convenience or arbitrary choice, but rather corresponds to a very strong statement about what the relevant output of the channel is.

   Read the original source
5. 

   eLife

   Aug 27, 2021

   Reviewer #2 (Public Review):

   My expertise is more on the theoretical than the experimental aspects of this paper, so those will be the focus of these comments.

   Signal transduction is an important area of study for mathematical biologists and biophysicists. This setting is a natural one for information-theoretic methods, and such methods are attracting increasing research interest. Experimental results that attempt to directly quantify the Shannon capacity of signal transduction are particularly interesting. This paper represents an important contribution to this emerging field.

   My main comments are about the rigorousness and correctness of the theoretical results. More details about these results would improve the paper and help the reader understand the results.

   The calculation of channel capacity, given in the methods, is quite a …

   Reviewer #2 (Public Review):

   My expertise is more on the theoretical than the experimental aspects of this paper, so those will be the focus of these comments.

   Signal transduction is an important area of study for mathematical biologists and biophysicists. This setting is a natural one for information-theoretic methods, and such methods are attracting increasing research interest. Experimental results that attempt to directly quantify the Shannon capacity of signal transduction are particularly interesting. This paper represents an important contribution to this emerging field.

   My main comments are about the rigorousness and correctness of the theoretical results. More details about these results would improve the paper and help the reader understand the results.

   The calculation of channel capacity, given in the methods, is quite a standard calculation and appears to be correct. However, I was confused by the use of the "weighting value" w_i, which is not specified in the manuscript. The input distribution appears to be a product of the weight w_i and the input probability value p_i, and these appear always to occur together as a product w_i p_i. (In joint probabilities w_i p(i,j), the input probability can be extracted using Bayes' rule, leaving w_i p_i p(j|i).) This leads met wonder two things. First, what role does w_i play (is it even necessary)? Second, of particular interest here is the capacity-achieving input distribution p_i, but w_i obscures it; is the physical input distribution p_i equal to the capacity-achieving distribution? If not, what is the meaning of capacity?

   A more minor but important point: the inputs and outputs of the communication channel are never explicitly defined, which makes the meaning of the results unclear. When evaluating the capacity of an information channel, the inputs X and outputs Y should be carefully defined, so that the mutual information I(X;Y) is meaningful; the mutual information is then maximized to obtain capacity. Although it can be inferred that the input X is the ligand concentration, and the output Y is the expression of GFP, it would be helpful if this were stated explicitly.

   Read the original source
6. 

   Version published to 10.1101/2021.05.10.443458v1 on bioRxiv

   May 10, 2021