Evaluating hippocampal replay without a ground truth
Curation statements for this article:-
Curated by eLife
eLife assessment
This work is a valuable presentation of sharp-wave-ripple reactivation of hippocampal neural ensemble activity recorded as animals explored two different environments. It attempts to use the fact that the ensemble code remaps between the two mazes to identify the best replay-detection procedures for analyzing this type of data. The reviewers found the evidence for a prescriptive conclusion inadequate, while still appreciating the concept of comparing maze-identity discrimination with replay.
This article has been Reviewed by the following groups
Discuss this preprint
Start a discussion What are Sciety discussions?Listed in
- Evaluated articles (eLife)
Abstract
During rest and sleep, memory traces replay in the brain. The dialogue between brain regions during replay is thought to stabilize labile memory traces for long-term storage. However, because replay is an internally driven, spontaneous phenomenon, it does not have a ground truth - an external reference that can validate whether a memory has truly been replayed. Instead, replay detection is based on the similarity between the sequential neural activity comprising the replay event and the corresponding template of neural activity generated during active locomotion. If the statistical likelihood of observing such a match by chance is sufficiently low, the candidate replay event is inferred to be replaying that specific memory. However, without the ability to evaluate whether replay detection methods are successfully detecting true events and correctly rejecting non-events, the evaluation and comparison of different replay methods is challenging. To circumvent this problem, we present a new framework for evaluating replay, tested using hippocampal neural recordings from rats exploring two novel linear tracks. Using this two-track paradigm, our framework selects replay events based on their temporal fidelity (sequence-based detection), and evaluates the detection performance using each event’s track discriminability, where sequenceless decoding across both tracks is used to quantify whether the track replaying is also the most likely track being reactivated.
Article activity feed
-

-

Author Response
Reviewer #1 (Public Review):
This work introduces a novel framework for evaluating the performance of statistical methods that identify replay events. This is challenging because hippocampal replay is a latent cognitive process, where the ground truth is inaccessible, so methods cannot be evaluated against a known answer. The framework consists of two elements:
- A replay sequence p-value, evaluated against shuffled permutations of the data, such as radon line fitting, rank-order correlation, or weighted correlation. This element determines how trajectory-like the spiking representation is. The p-value threshold for all accepted replay events is adjusted based on an empirical shuffled distribution to control for the false discovery rate.
- A trajectory discriminability score, also evaluated against shuffled …
Author Response
Reviewer #1 (Public Review):
This work introduces a novel framework for evaluating the performance of statistical methods that identify replay events. This is challenging because hippocampal replay is a latent cognitive process, where the ground truth is inaccessible, so methods cannot be evaluated against a known answer. The framework consists of two elements:
- A replay sequence p-value, evaluated against shuffled permutations of the data, such as radon line fitting, rank-order correlation, or weighted correlation. This element determines how trajectory-like the spiking representation is. The p-value threshold for all accepted replay events is adjusted based on an empirical shuffled distribution to control for the false discovery rate.
- A trajectory discriminability score, also evaluated against shuffled permutations of the data. In this case, there are two different possible spatial environments that can be replayed, so the method compares the log odds of track 1 vs. track 2.
The authors then use this framework (accepted number of replay events and trajectory discriminability) to study the performance of replay identification methods. They conclude that sharp wave ripple power is not a necessary criterion for identifying replay event candidates during awake run behavior if you have high multiunit activity, a higher number of permutations is better for identifying replay events, linear Bayesian decoding methods outperform rank-order correlation, and there is no evidence for pre-play.
The authors tackle a difficult and important problem for those studying hippocampal replay (and indeed all latent cognitive processes in the brain) with spiking data: how do we understand how well our methods are doing when the ground truth is inaccessible? Additionally, systematically studying how the variety of methods for identifying replay perform, is important for understanding the sometimes contradictory conclusions from replay papers. It helps consolidate the field around particular methods, leading to better reproducibility in the future. The authors' framework is also simple to implement and understand and the code has been provided, making it accessible to other neuroscientists. Testing for track discriminability, as well as the sequentiality of the replay event, is a sensible additional data point to eliminate "spurious" replay events.
However, there are some concerns with the framework as well. The novelty of the framework is questionable as it consists of a log odds measure previously used in two prior papers (Carey et al. 2019 and the authors' own Tirole & Huelin Gorriz, et al., 2022) and a multiple comparisons correction, albeit a unique empirical multiple comparisons correction based on shuffled data.
With respect to the log odds measure itself, as presented, it is reliant on having only two options to test between, limiting its general applicability. Even in the data used for the paper, there are sometimes three tracks, which could influence the conclusions of the paper about the validity of replay methods. This also highlights a weakness of the method in that it assumes that the true model (spatial track environment) is present in the set of options being tested. Furthermore, the log odds measure itself is sensitive to the defined ripple or multiunit start and end times, because it marginalizes over both position and time, so any inclusion of place cells that fire for the animal's stationary position could influence the discriminability of the track. Multiple track representations during a candidate replay event would also limit track discriminability. Finally, the authors call this measure "trajectory discriminability", which seems a misnomer as the time and position information are integrated out, so there is no notion of trajectory.
The authors also fail to make the connection with the control of the false discovery rate via false positives on empirical shuffles with existing multiple comparison corrections that control for false discovery rates (such as the Benjamini and Hochberg procedure or Storey's q-value). Additionally, the particular type of shuffle used will influence the empirically determined p-value, making the procedure dependent on the defined null distribution. Shuffling the data is also considerably more computationally intensive than the existing multiple comparison corrections.
Overall, the authors make interesting conclusions with respect to hippocampal replay methods, but the utility of the method is limited in scope because of its reliance on having exactly two comparisons and having to specify the null distribution to control for the false discovery rate. This work will be of interest to electrophysiologists studying hippocampal replay in spiking data.
We would like to thank the reviewer for the feedback.
Firstly, we would like to clarify that it is not our intention to present this tool as a novel replay detection approach. It is indeed merely a novel tool for evaluating different replay detection methods. Also, while we previously used log odds metrics to quantify contextual discriminability within replay events (Tirole et al., 2021), this framework is novel in how it is used (to compare replay detection methods), and the use of empirically determined FPR-matched alpha levels. We have now modified the manuscript to make this point more explicit.
Our use of the term trajectory-discriminability is now changed to track-discriminability in the revised manuscript, given we are summing over time and space, as correctly pointed out by the reviewer.
While this approach requires two tracks in its current implementation, we have also been able to apply this approach to three tracks, with a minor variation in the method, however this is beyond the scope of our current manuscript. Prior experience on other tracks not analysed in the log odds calculation should not pose any issue, given that the animal likely replays many experiences of the day (e.g. the homecage). These “other” replay events likely contribute to candidate replay events that fail to have a statistically significant replay score on either track.
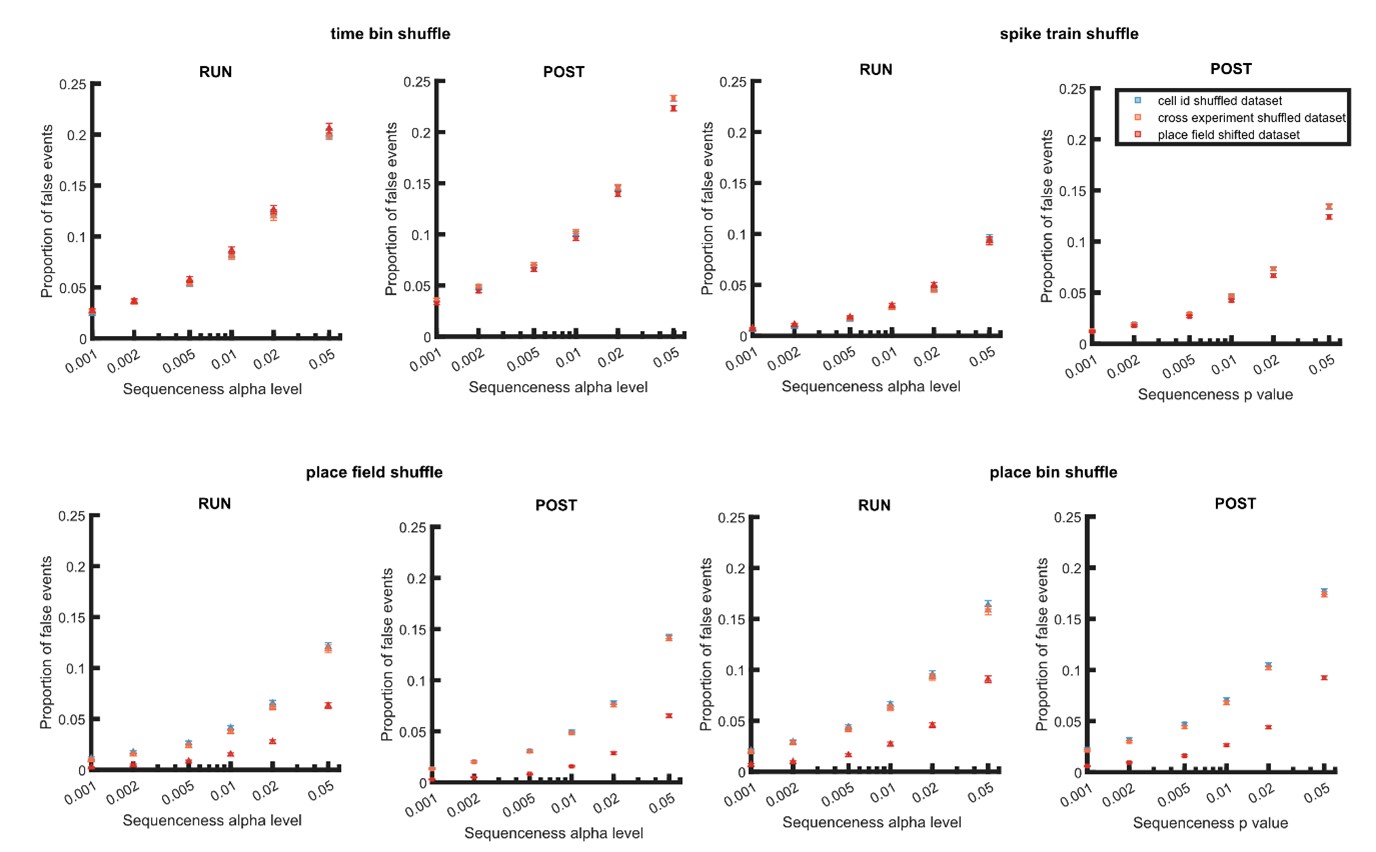
With regard to using a cell-id randomized dataset to empirically estimate false-positive rates, we have provided a detailed explanation behind our choice of using an alpha level correction in our response to the essential revisions above. This approach is not used to examine the effect of multiple comparisons, but rather to measure the replay detection error due to non-independence and a non-uniform p value distribution. Therefore we do not believe that existing multiple comparison corrections such as Benjamini and Hochberg procedure are applicable here (Author response image 1-3). Given the potential issues raised with a session-based cell-id randomization, we demonstrate above that the null distribution is sufficiently independent from the four shuffle-types used for replay detection (the same was not true for a place field randomized dataset) (Author response image 4).
Author response image 1.
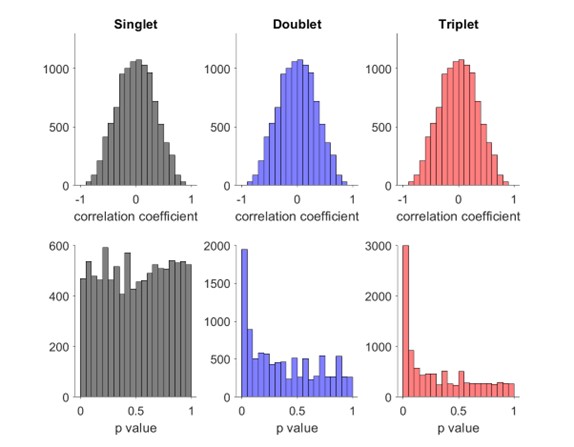
Distribution of Spearman’s rank order correlation score and p value for false events with random sequence where each neuron fires one (left), two (middle) or three (right) spikes.
Author response image 2.
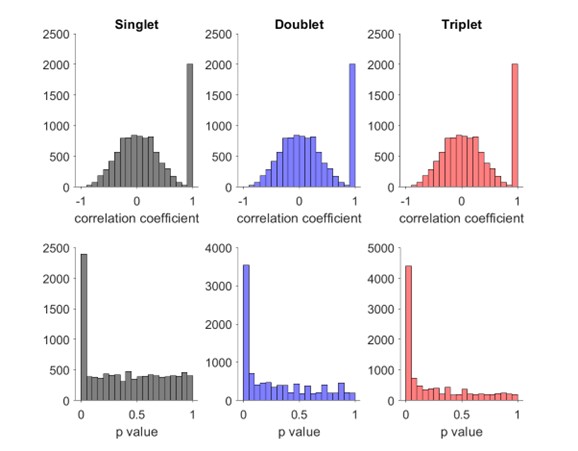
Distribution of Spearman’s rank order correlation score and p value for mixture of 20% true events and 80% false events where each neuron fires one (left), two (middle) or three (right) spikes.
Author response image 3.
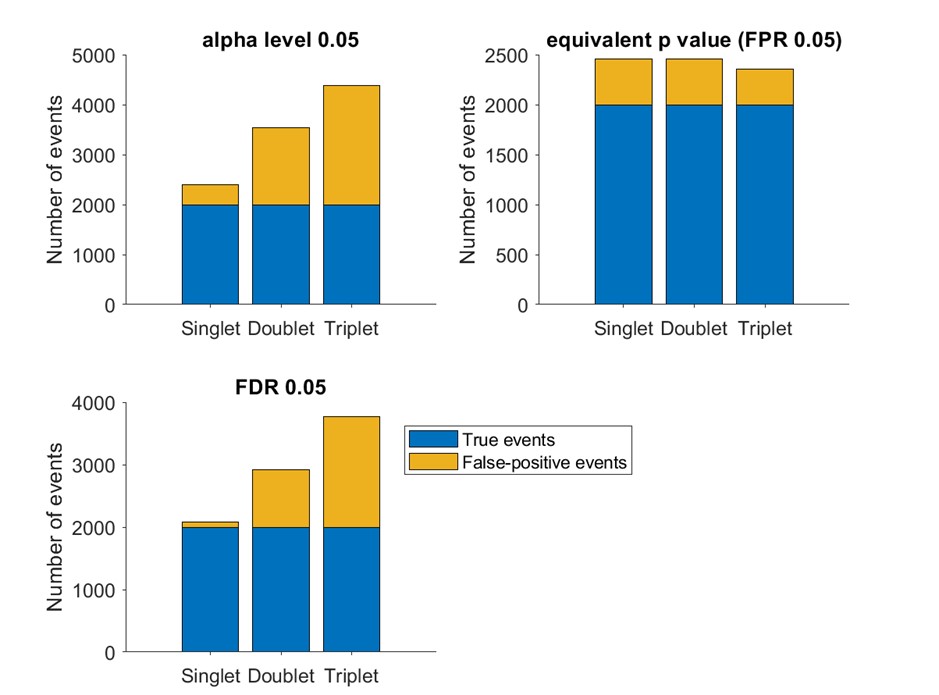
Number of true events (blue) and false events (yellow) detected based on alpha level 0.05 (upper left), empirical false positive rate 5% (upper right) and false discovery rate 5% (lower left, based on BH method)
Author response image 4.
Proportion of false events detected when using dataset with within and cross experiment cell-id randomization and place field randomization. The detection was based on single shuffle including time bin permutation shuffle, spike train circular shift shuffle, place field circular shift shuffle, and place bin circular shift shuffle.
Reviewer #2 (Public Review):
This study proposes to evaluate and compare different replay methods in the absence of "ground truth" using data from hippocampal recordings of rodents that were exposed to two different tracks on the same day. The study proposes to leverage the potential of Bayesian methods to decode replay and reactivation in the same events. They find that events that pass a higher threshold for replay typically yield a higher measure of reactivation. On the other hand, events from the shuffled data that pass thresholds for replay typically don't show any reactivation. While well-intentioned, I think the result is highly problematic and poorly conceived.
The work presents a lot of confusion about the nature of null hypothesis testing and the meaning of p-values. The prescription arrived at, to correct p-values by putting animals on two separate tracks and calculating a "sequence-less" measure of reactivation are impractical from an experimental point of view, and unsupportable from a statistical point of view. Much of the observations are presented as solutions for the field, but are in fact highly dependent on distinct features of the dataset at hand. The most interesting observation is that despite the existence of apparent sequences in the PRE-RUN data, no reactivation is detectable in those events, suggesting that in fact they represent spurious events. I would recommend the authors focus on this important observation and abandon the rest of the work, as it has the potential to further befuddle and promote poor statistical practices in the field.
The major issue is that the manuscript conveys much confusion about the nature of hypothesis testing and the meaning of p-values. It's worth stating here the definition of a p-value: the conditional probability of rejecting the null hypothesis given that the null hypothesis is true. Unfortunately, in places, this study appears to confound the meaning of the p-value with the probability of rejecting the null hypothesis given that the null hypothesis is NOT true-i.e. in their recordings from awake replay on different mazes. Most of their analysis is based on the observation that events that have higher reactivation scores, as reflected in the mean log odds differences, have lower p-values resulting from their replay analyses. Shuffled data, in contrast, does not show any reactivation but can still show spurious replays depending on the shuffle procedure used to create the surrogate dataset. The authors suggest using this to test different practices in replay detection. However, another important point that seems lost in this study is that the surrogate dataset that is contrasted with the actual data depends very specifically on the null hypothesis that is being tested. That is to say, each different shuffle procedure is in fact testing a different null hypothesis. Unfortunately, most studies, including this one, are not very explicit about which null hypothesis is being tested with a given resampling method, but the p-value obtained is only meaningful insofar as the null that is being tested and related assumptions are clearly understood. From a statistical point of view, it makes no sense to adjust the p-value obtained by one shuffle procedure according to the p-value obtained by a different shuffle procedure, which is what this study inappropriately proposes. Other prescriptions offered by the study are highly dataset and method dependent and discuss minutiae of event detection, such as whether or not to require power in the ripple frequency band.
We would like to thank the reviewer for their feedback. The purpose of this paper is to present a novel tool for evaluating replay sequence detection using an independent measure that does not depend on the sequence score. As the reviewer stated, in this study, we are detecting replay events based on a set alpha threshold (0.05), based on the conditional probability of rejecting the null hypothesis given that the null hypothesis is true. For all replay events detected during PRE, RUN or POST, they are classified as track 1 or track 2 replay events by comparing each event’s sequence score relative to the shuffled distribution. Then, the log odds measure was only applied to track 1 and track 2 replay events selected using sequence-based detection. Its important to clarify that we never use log odds to select events to examine their sequenceness p value. Therefore, we disagree with the reviewer’s claim that for awake replay events detected on different tracks, we are quantifying the probability of rejecting the null hypothesis given that the null hypothesis is not true.
However, we fully understand the reviewer’s concerns with a cell-id randomization, and the potential caveats associated with using this approach for quantifying the false positive rate. First of all, we would like to clarify that the purpose of alpha level adjustment was to facilitate comparison across methods by finding the alpha level with matching false-positive rates determined empirically. Without doing this, it is impossible to compare two methods that differ in strictness (e.g. is using two different shuffles needed compared to using a single shuffle procedure). This means we are interested in comparing the performance of different methods at the equivalent alpha level where each method detects 5% spurious events per track rather than an arbitrary alpha level of 0.05 (which is difficult to interpret if statistical tests are run on non-independent samples). Once the false positive rate is matched, it is possible to compare two methods to see which one yields more events and/or has better track discriminability.
We agree with the reviewer that the choice of data randomization is crucial. When a null distribution of a randomized dataset is very similar to the null distribution used for detection, this should lead to a 5% false positive rate (as a consequence of circular reasoning). In our response to the essential revisions, we have discussed about the effect of data randomization on replay detection. We observed that while place field circularly shifted dataset and cell-id randomized dataset led to similar false-positive rates when shuffles that disrupt temporal information were used for detection, a place field circularly shifted dataset but not a cell-id randomized dataset was sensitive to shuffle methods that disrupted place information (Author response image 4). We would also like to highlight one of our findings from the manuscript that the discrepancy between different methods can be substantially reduced when alpha level was adjusted to match false-positive rates (Figure 6B). This result directly supports the utility of a cell-id randomized dataset in finding the alpha level with equivalent false positive rates across methods. Hence, while imperfect, we argue cell-id randomization remains an acceptable method as it is sufficiently different from the four shuffles we used for replay detection compared to place field randomized dataset (Author response image 4).
While the use of two linear tracks was crucial for our current framework to calculate log odds for evaluating replay detection, we acknowledge that it limits the applicability of this framework. At the same time, the conclusions of the manuscript with regard to ripples, replay methods, and preplay should remain valid on a single track. A second track just provides a useful control for how place cells can realistically remap within another environment. However, with modification, it may be applied to a maze with different arms or subregions, although this is beyond the scope of our current study.
Last of not least, we partly agree with the reviewer that the result can be dataset-specific such that the result may vary depending on animal’s behavioural state and experimental design. However, our results highlight the fact that there is a very wide distribution of both the track discriminability and the proportion of significant events detected across methods that are currently used in the field. And while we see several methods that appear comparable in their effectiveness in replay detection, there are also other methods that are deeply flawed (that have been previously been used in peer-reviewed publications) if the alpha level is not sufficiently strict. Regardless of the method used, most methods can be corrected with an appropriate alpha level (e.g. using all spikes for a rank order correlation). Therefore, while the exact result may be dataset-specific, we feel that this is most likely due to the number of cells and properties of the track more than the use of two tracks. Reporting of the empirically determined false-positive rate and use of alpha level with matching false-positive rate (such as 0.05) for detection does not require a second track, and the adoption of this approach by other labs would help to improve the interpretability and generalizability of their replay data.
Reviewer #3 (Public Review):
This study tackles a major problem with replay detection, which is that different methods can produce vastly different results. It provides compelling evidence that the source of this inconsistency is that biological data often violates assumptions of independent samples. This results in false positive rates that can vary greatly with the precise statistical assumptions of the chosen replay measure, the detection parameters, and the dataset itself. To address this issue, the authors propose to empirically estimate the false positive rate and control for it by adjusting the significance threshold. Remarkably, this reconciles the differences in replay detection methods, as the results of all the replay methods tested converge quite well (see Figure 6B). This suggests that by controlling for the false positive rate, one can get an accurate estimate of replay with any of the standard methods.
When comparing different replay detection methods, the authors use a sequence-independent log-odds difference score as a validation tool and an indirect measure of replay quality. This takes advantage of the two-track design of the experimental data, and its use here relies on the assumption that a true replay event would be associated with good (discriminable) reactivation of the environment that is being replayed. The other way replay "quality" is estimated is by the number of replay events detected once the false positive rate is taken into account. In this scheme, "better" replay is in the top right corner of Figure 6B: many detected events associated with congruent reactivation.
There are two possible ways the results from this study can be integrated into future replay research. The first, simpler, way is to take note of the empirically estimated false positive rates reported here and simply avoid the methods that result in high false positive rates (weighted correlation with a place bin shuffle or all-spike Spearman correlation with a spike-id shuffle). The second, perhaps more desirable, way is to integrate the practice of estimating the false positive rate when scoring replay and to take it into account. This is very powerful as it can be applied to any replay method with any choice of parameters and get an accurate estimate of replay.
How does one estimate the false positive rate in their dataset? The authors propose to use a cell-ID shuffle, which preserves all the firing statistics of replay events (bursts of spikes by the same cell, multi-unit fluctuations, etc.) but randomly swaps the cells' place fields, and to repeat the replay detection on this surrogate randomized dataset. Of course, there is no perfect shuffle, and it is possible that a surrogate dataset based on this particular shuffle may result in one underestimating the true false positive rate if different cell types are present (e.g. place field statistics may differ between CA1 and CA3 cells, or deep vs. superficial CA1 cells, or place cells vs. non-place cells if inclusion criteria are not strict). Moreover, it is crucial that this validation shuffle be independent of any shuffling procedure used to determine replay itself (which may not always be the case, particularly for the pre-decoding place field circular shuffle used by some of the methods here) lest the true false-positive rate be underestimated. Once the false positive rate is estimated, there are different ways one may choose to control for it: adjusting the significance threshold as the current study proposes, or directly comparing the number of events detected in the original vs surrogate data. Either way, with these caveats in mind, controlling for the false positive rate to the best of our ability is a powerful approach that the field should integrate.
Which replay detection method performed the best? If one does not control for varying false positive rates, there are two methods that resulted in strikingly high (>15%) false positive rates: these were weighted correlation with a place bin shuffle and Spearman correlation (using all spikes) with a spike-id shuffle. However, after controlling for the false positive rate (Figure 6B) all methods largely agree, including those with initially high false positive rates. There is no clear "winner" method, because there is a lot of overlap in the confidence intervals, and there also are some additional reasons for not overly interpreting small differences in the observed results between methods. The confidence intervals are likely to underestimate the true variance in the data because the resampling procedure does not involve hierarchical statistics and thus fails to account for statistical dependencies on the session and animal level. Moreover, it is possible that methods that involve shuffles similar to the cross-validation shuffle ("wcorr 2 shuffles", "wcorr 3 shuffles" both use a pre-decoding place field circular shuffle, which is very similar to the pre-decoding place field swap used in the cross-validation procedure to estimate the false positive rate) may underestimate the false positive rate and therefore inflate adjusted p-value and the proportion of significant events. We should therefore not interpret small differences in the measured values between methods, and the only clear winner and the best way to score replay is using any method after taking the empirically estimated false positive rate into account.
The authors recommend excluding low-ripple power events in sleep, because no replay was observed in events with low (0-3 z-units) ripple power specifically in sleep, but that no ripple restriction is necessary for awake events. There are problems with this conclusion. First, ripple power is not the only way to detect sharp-wave ripples (the sharp wave is very informative in detecting awake events). Second, when talking about sequence quality in awake non-ripple data, it is imperative for one to exclude theta sequences. The authors' speed threshold of 5 cm/s is not sufficient to guarantee that no theta cycles contaminate the awake replay events. Third, a direct comparison of the results with and without exclusion is lacking (selecting for the lower ripple power events is not the same as not having a threshold), so it is unclear how crucial it is to exclude the minority of the sleep events outside of ripples. The decision of whether or not to select for ripples should depend on the particular study and experimental conditions that can affect this measure (electrode placement, brain state prevalence, noise levels, etc.).
Finally, the authors address a controversial topic of de-novo preplay. With replay detection corrected for the false positive rate, none of the detection methods produce evidence of preplay sequences nor sequenceless reactivation in the tested dataset. This presents compelling evidence in favour of the view that the sequence of place fields formed on a novel track cannot be predicted by the sequential structure found in pre-task sleep.
We would like to thank the reviewer for the positive and constructive feedback.
We agree with the reviewer that the conclusion about the effect of ripple power is dataset-specific and is not intended to be a one-size-fit-all recommendation for wider application. But it does raise a concern that individual studies should address. The criteria used for selecting candidate events will impact the overall fraction of detected events, and makes the comparison between studies using different methods more difficult. We have updated the manuscript to emphasize this point.
“These results emphasize that a ripple power threshold is not necessary for RUN replay events in our dataset but may still be beneficial, as long as it does not excessively eliminate too many good replay events with low ripple power. In other words, depending on the experimental design, it is possible that a stricter p-value with no ripple threshold can be used to detect more replay events than using a less strict p-value combined with a strict ripple power threshold. However, for POST replay events, a threshold at least in the range of a z-score of 3-5 is recommended based on our dataset, to reduce inclusion of false-positives within the pool of detected replay events.”
“We make six key observations: 1) A ripple power threshold may be more important for replay events during POST compared to RUN. For our dataset, the POST replay events with ripple power below a z-score of 3-5 were indistinguishable from spurious events. While the exact ripple z-score threshold to implement may differ depending on the experimental condition (e.g. electrode placement, behavioural paradigm, noise level and etc) and experimental aim, our findings highlight the benefit of using ripple power threshold for detecting replay during POST.
- ”
-

eLife assessment
This work is a valuable presentation of sharp-wave-ripple reactivation of hippocampal neural ensemble activity recorded as animals explored two different environments. It attempts to use the fact that the ensemble code remaps between the two mazes to identify the best replay-detection procedures for analyzing this type of data. The reviewers found the evidence for a prescriptive conclusion inadequate, while still appreciating the concept of comparing maze-identity discrimination with replay.
-

Reviewer #1 (Public Review):
This work introduces a novel framework for evaluating the performance of statistical methods that identify replay events. This is challenging because hippocampal replay is a latent cognitive process, where the ground truth is inaccessible, so methods cannot be evaluated against a known answer. The framework consists of two elements:
1. A replay sequence p-value, evaluated against shuffled permutations of the data, such as radon line fitting, rank-order correlation, or weighted correlation. This element determines how trajectory-like the spiking representation is. The p-value threshold for all accepted replay events is adjusted based on an empirical shuffled distribution to control for the false discovery rate.
2. A trajectory discriminability score, also evaluated against shuffled permutations of the data. …Reviewer #1 (Public Review):
This work introduces a novel framework for evaluating the performance of statistical methods that identify replay events. This is challenging because hippocampal replay is a latent cognitive process, where the ground truth is inaccessible, so methods cannot be evaluated against a known answer. The framework consists of two elements:
1. A replay sequence p-value, evaluated against shuffled permutations of the data, such as radon line fitting, rank-order correlation, or weighted correlation. This element determines how trajectory-like the spiking representation is. The p-value threshold for all accepted replay events is adjusted based on an empirical shuffled distribution to control for the false discovery rate.
2. A trajectory discriminability score, also evaluated against shuffled permutations of the data. In this case, there are two different possible spatial environments that can be replayed, so the method compares the log odds of track 1 vs. track 2.The authors then use this framework (accepted number of replay events and trajectory discriminability) to study the performance of replay identification methods. They conclude that sharp wave ripple power is not a necessary criterion for identifying replay event candidates during awake run behavior if you have high multiunit activity, a higher number of permutations is better for identifying replay events, linear Bayesian decoding methods outperform rank-order correlation, and there is no evidence for pre-play.
The authors tackle a difficult and important problem for those studying hippocampal replay (and indeed all latent cognitive processes in the brain) with spiking data: how do we understand how well our methods are doing when the ground truth is inaccessible? Additionally, systematically studying how the variety of methods for identifying replay perform, is important for understanding the sometimes contradictory conclusions from replay papers. It helps consolidate the field around particular methods, leading to better reproducibility in the future. The authors' framework is also simple to implement and understand and the code has been provided, making it accessible to other neuroscientists. Testing for track discriminability, as well as the sequentiality of the replay event, is a sensible additional data point to eliminate "spurious" replay events.
However, there are some concerns with the framework as well. The novelty of the framework is questionable as it consists of a log odds measure previously used in two prior papers (Carey et al. 2019 and the authors' own Tirole & Huelin Gorriz, et al., 2022) and a multiple comparisons correction, albeit a unique empirical multiple comparisons correction based on shuffled data.
With respect to the log odds measure itself, as presented, it is reliant on having only two options to test between, limiting its general applicability. Even in the data used for the paper, there are sometimes three tracks, which could influence the conclusions of the paper about the validity of replay methods. This also highlights a weakness of the method in that it assumes that the true model (spatial track environment) is present in the set of options being tested. Furthermore, the log odds measure itself is sensitive to the defined ripple or multiunit start and end times, because it marginalizes over both position and time, so any inclusion of place cells that fire for the animal's stationary position could influence the discriminability of the track. Multiple track representations during a candidate replay event would also limit track discriminability. Finally, the authors call this measure "trajectory discriminability", which seems a misnomer as the time and position information are integrated out, so there is no notion of trajectory.
The authors also fail to make the connection with the control of the false discovery rate via false positives on empirical shuffles with existing multiple comparison corrections that control for false discovery rates (such as the Benjamini and Hochberg procedure or Storey's q-value). Additionally, the particular type of shuffle used will influence the empirically determined p-value, making the procedure dependent on the defined null distribution. Shuffling the data is also considerably more computationally intensive than the existing multiple comparison corrections.
Overall, the authors make interesting conclusions with respect to hippocampal replay methods, but the utility of the method is limited in scope because of its reliance on having exactly two comparisons and having to specify the null distribution to control for the false discovery rate. This work will be of interest to electrophysiologists studying hippocampal replay in spiking data.
-

Reviewer #2 (Public Review):
This study proposes to evaluate and compare different replay methods in the absence of "ground truth" using data from hippocampal recordings of rodents that were exposed to two different tracks on the same day. The study proposes to leverage the potential of Bayesian methods to decode replay and reactivation in the same events. They find that events that pass a higher threshold for replay typically yield a higher measure of reactivation. On the other hand, events from the shuffled data that pass thresholds for replay typically don't show any reactivation. While well-intentioned, I think the result is highly problematic and poorly conceived.
The work presents a lot of confusion about the nature of null hypothesis testing and the meaning of p-values. The prescription arrived at, to correct p-values by putting …
Reviewer #2 (Public Review):
This study proposes to evaluate and compare different replay methods in the absence of "ground truth" using data from hippocampal recordings of rodents that were exposed to two different tracks on the same day. The study proposes to leverage the potential of Bayesian methods to decode replay and reactivation in the same events. They find that events that pass a higher threshold for replay typically yield a higher measure of reactivation. On the other hand, events from the shuffled data that pass thresholds for replay typically don't show any reactivation. While well-intentioned, I think the result is highly problematic and poorly conceived.
The work presents a lot of confusion about the nature of null hypothesis testing and the meaning of p-values. The prescription arrived at, to correct p-values by putting animals on two separate tracks and calculating a "sequence-less" measure of reactivation are impractical from an experimental point of view, and unsupportable from a statistical point of view. Much of the observations are presented as solutions for the field, but are in fact highly dependent on distinct features of the dataset at hand. The most interesting observation is that despite the existence of apparent sequences in the PRE-RUN data, no reactivation is detectable in those events, suggesting that in fact they represent spurious events. I would recommend the authors focus on this important observation and abandon the rest of the work, as it has the potential to further befuddle and promote poor statistical practices in the field.
The major issue is that the manuscript conveys much confusion about the nature of hypothesis testing and the meaning of p-values. It's worth stating here the definition of a p-value: the conditional probability of rejecting the null hypothesis given that the null hypothesis is true. Unfortunately, in places, this study appears to confound the meaning of the p-value with the probability of rejecting the null hypothesis given that the null hypothesis is NOT true-i.e. in their recordings from awake replay on different mazes. Most of their analysis is based on the observation that events that have higher reactivation scores, as reflected in the mean log odds differences, have lower p-values resulting from their replay analyses. Shuffled data, in contrast, does not show any reactivation but can still show spurious replays depending on the shuffle procedure used to create the surrogate dataset. The authors suggest using this to test different practices in replay detection. However, another important point that seems lost in this study is that the surrogate dataset that is contrasted with the actual data depends very specifically on the null hypothesis that is being tested. That is to say, each different shuffle procedure is in fact testing a different null hypothesis. Unfortunately, most studies, including this one, are not very explicit about which null hypothesis is being tested with a given resampling method, but the p-value obtained is only meaningful insofar as the null that is being tested and related assumptions are clearly understood. From a statistical point of view, it makes no sense to adjust the p-value obtained by one shuffle procedure according to the p-value obtained by a different shuffle procedure, which is what this study inappropriately proposes. Other prescriptions offered by the study are highly dataset and method dependent and discuss minutiae of event detection, such as whether or not to require power in the ripple frequency band.
-

Reviewer #3 (Public Review):
This study tackles a major problem with replay detection, which is that different methods can produce vastly different results. It provides compelling evidence that the source of this inconsistency is that biological data often violates assumptions of independent samples. This results in false positive rates that can vary greatly with the precise statistical assumptions of the chosen replay measure, the detection parameters, and the dataset itself. To address this issue, the authors propose to empirically estimate the false positive rate and control for it by adjusting the significance threshold. Remarkably, this reconciles the differences in replay detection methods, as the results of all the replay methods tested converge quite well (see Figure 6B). This suggests that by controlling for the false positive …
Reviewer #3 (Public Review):
This study tackles a major problem with replay detection, which is that different methods can produce vastly different results. It provides compelling evidence that the source of this inconsistency is that biological data often violates assumptions of independent samples. This results in false positive rates that can vary greatly with the precise statistical assumptions of the chosen replay measure, the detection parameters, and the dataset itself. To address this issue, the authors propose to empirically estimate the false positive rate and control for it by adjusting the significance threshold. Remarkably, this reconciles the differences in replay detection methods, as the results of all the replay methods tested converge quite well (see Figure 6B). This suggests that by controlling for the false positive rate, one can get an accurate estimate of replay with any of the standard methods.
When comparing different replay detection methods, the authors use a sequence-independent log-odds difference score as a validation tool and an indirect measure of replay quality. This takes advantage of the two-track design of the experimental data, and its use here relies on the assumption that a true replay event would be associated with good (discriminable) reactivation of the environment that is being replayed. The other way replay "quality" is estimated is by the number of replay events detected once the false positive rate is taken into account. In this scheme, "better" replay is in the top right corner of Figure 6B: many detected events associated with congruent reactivation.
There are two possible ways the results from this study can be integrated into future replay research. The first, simpler, way is to take note of the empirically estimated false positive rates reported here and simply avoid the methods that result in high false positive rates (weighted correlation with a place bin shuffle or all-spike Spearman correlation with a spike-id shuffle). The second, perhaps more desirable, way is to integrate the practice of estimating the false positive rate when scoring replay and to take it into account. This is very powerful as it can be applied to any replay method with any choice of parameters and get an accurate estimate of replay.
How does one estimate the false positive rate in their dataset? The authors propose to use a cell-ID shuffle, which preserves all the firing statistics of replay events (bursts of spikes by the same cell, multi-unit fluctuations, etc.) but randomly swaps the cells' place fields, and to repeat the replay detection on this surrogate randomized dataset. Of course, there is no perfect shuffle, and it is possible that a surrogate dataset based on this particular shuffle may result in one underestimating the true false positive rate if different cell types are present (e.g. place field statistics may differ between CA1 and CA3 cells, or deep vs. superficial CA1 cells, or place cells vs. non-place cells if inclusion criteria are not strict). Moreover, it is crucial that this validation shuffle be independent of any shuffling procedure used to determine replay itself (which may not always be the case, particularly for the pre-decoding place field circular shuffle used by some of the methods here) lest the true false-positive rate be underestimated. Once the false positive rate is estimated, there are different ways one may choose to control for it: adjusting the significance threshold as the current study proposes, or directly comparing the number of events detected in the original vs surrogate data. Either way, with these caveats in mind, controlling for the false positive rate to the best of our ability is a powerful approach that the field should integrate.
Which replay detection method performed the best? If one does not control for varying false positive rates, there are two methods that resulted in strikingly high (>15%) false positive rates: these were weighted correlation with a place bin shuffle and Spearman correlation (using all spikes) with a spike-id shuffle. However, after controlling for the false positive rate (Figure 6B) all methods largely agree, including those with initially high false positive rates. There is no clear "winner" method, because there is a lot of overlap in the confidence intervals, and there also are some additional reasons for not overly interpreting small differences in the observed results between methods. The confidence intervals are likely to underestimate the true variance in the data because the resampling procedure does not involve hierarchical statistics and thus fails to account for statistical dependencies on the session and animal level. Moreover, it is possible that methods that involve shuffles similar to the cross-validation shuffle ("wcorr 2 shuffles", "wcorr 3 shuffles" both use a pre-decoding place field circular shuffle, which is very similar to the pre-decoding place field swap used in the cross-validation procedure to estimate the false positive rate) may underestimate the false positive rate and therefore inflate adjusted p-value and the proportion of significant events. We should therefore not interpret small differences in the measured values between methods, and the only clear winner and the best way to score replay is using any method after taking the empirically estimated false positive rate into account.
The authors recommend excluding low-ripple power events in sleep, because no replay was observed in events with low (0-3 z-units) ripple power specifically in sleep, but that no ripple restriction is necessary for awake events. There are problems with this conclusion. First, ripple power is not the only way to detect sharp-wave ripples (the sharp wave is very informative in detecting awake events). Second, when talking about sequence quality in awake non-ripple data, it is imperative for one to exclude theta sequences. The authors' speed threshold of 5 cm/s is not sufficient to guarantee that no theta cycles contaminate the awake replay events. Third, a direct comparison of the results with and without exclusion is lacking (selecting for the lower ripple power events is not the same as not having a threshold), so it is unclear how crucial it is to exclude the minority of the sleep events outside of ripples. The decision of whether or not to select for ripples should depend on the particular study and experimental conditions that can affect this measure (electrode placement, brain state prevalence, noise levels, etc.).
Finally, the authors address a controversial topic of de-novo preplay. With replay detection corrected for the false positive rate, none of the detection methods produce evidence of preplay sequences nor sequenceless reactivation in the tested dataset. This presents compelling evidence in favour of the view that the sequence of place fields formed on a novel track cannot be predicted by the sequential structure found in pre-task sleep.
-