A theory of synaptic transmission

Article activity feed

1. 

   eLife

   Jul 18, 2022

   Author Response

   Reviewer #1 (Public Review):

   Wang and Dudko derive analytical equations for one special case of a model of Ca-dependent vesicle fusion, in the attempt to find a "general theory" of synaptic transmission. They use a model with 2 kinetically distinct fast and slow pools (equation 1).

   Critique

   1. Overall, the analytical approach applied here remains limited to the quite arbitrarily chosen 2-pool model. Thus, while the authors are able to re-capitulate the kinetics of transmitter release under a series of defined intracellular Ca-concentration steps, [Ca]i (see Fig. 2B; data from Woelfel et al. 2007 J. Neuroscience), this is nevertheless not surprising because the data by Woelfel et al. was originally also fit with a 2-pool model. More importantly, the 2-pool model is valid for describing release kinetics at high [Ca]i, …

   Author Response

   Reviewer #1 (Public Review):

   Wang and Dudko derive analytical equations for one special case of a model of Ca-dependent vesicle fusion, in the attempt to find a "general theory" of synaptic transmission. They use a model with 2 kinetically distinct fast and slow pools (equation 1).

   Critique

   1. Overall, the analytical approach applied here remains limited to the quite arbitrarily chosen 2-pool model. Thus, while the authors are able to re-capitulate the kinetics of transmitter release under a series of defined intracellular Ca-concentration steps, [Ca]i (see Fig. 2B; data from Woelfel et al. 2007 J. Neuroscience), this is nevertheless not surprising because the data by Woelfel et al. was originally also fit with a 2-pool model. More importantly, the 2-pool model is valid for describing release kinetics at high [Ca]i, but it cannot account for other important phenomena of synaptic transmission like e.g. spontaneous and asynchronous release which happen at lower [Ca]i, with different Ca cooperativity (Lou et al., 2005). Along the same lines, the derivations of the equations by Wang and Dudko are not valid in the range of low [Ca]i below about 1 micromolar (see "private recommendations" for details). This, however, limits the applicability of the model to AP-driven transmitter release, and it shows that based on one specific arbitrarily chosen model (here: the 2-pool model), one cannot claim to build a realistic and full "theory" for synaptic transmission.

   Our two-pool description is far from being “arbitrarily chosen”. It is based on experimental facts that have been established by multiple independent laboratories: namely, the observed two distinct vesicle fusion kinetics due to the presence of the readily releasable and reserve pools in vivo and due to the presence of two dominant vesicle morphologies in vitro. The two-pool picture has been confirmed and successfully used in numerous experimental papers previously. That being said, our two-pool description refers to a more general notion of separation of timescales and is thus more flexible than a literal interpretation might suggest.

   The data from Woelfel et al. 2007 J. Neuroscience, while of excellent quality, are not the only measured kinetics of the action-potential triggered vesicle fusion that our theory has been able to recapitulate (see other experimental data in Fig.2 and Fig.3 of the manuscript). The theory also recapitulates the kinetic measurements from fifteen other independent experimental studies, on ten different types of synapses. The dynamic range (peak release rate) of these synapses vary by 10 orders of magnitude, and the range of Ca2+ concentrations spans more than 3 orders of magnitude. Our work recapitulates these 16 datasets not through 16 different ad-hoc models but through a single, fully analytically solved, theoretical framework. Importantly, beyond recapitulating the existing data, our analytically tractable theory enables one to extract the unique sets of microscopic parameters for particular synapses, such as the activation energies and kinetic rates of their synaptic machinery, the sizes of the vesicle pools and the critical number of SNAREs. We verify that these predictions from our theory have reasonable values for each of the data sets; this is an additional, non-trivial check of our theory. The fact that our theory reproduces observations on such strikingly diverse systems, and has such a degree of predictive power, cannot be dismissed as an artifact or coincidence. We are not aware of any other theory, nor fitting model, of comparable generality and the ability to generate concrete predictions.

   Reviewer #1 is mistaken in stating that the derivations of our equations are not valid below 1 micromolar Ca2+ concentrations. It is evident already from Figure R1 below (Fig.2 in the revised manuscript) that the theory performs flawlessly at concentrations as low as 0.1µM. There are indeed non-linear effects at ultra-low Ca2+ concentrations that are not displayed by the experimental data in Fig. R1. Our theory is also applicable in that regime: one simply needs to include a second coordinate (in addition to the number of Ca2+ ions bound, 𝑄‡ ) to account for the multidimensionality of the free energy landscape, analogous to the calculations of the rate constants for multidimensional activated rate processes in chemical physics. This illustrates just one of the many ways in which our theory will enable detailed studies of mechanistic aspects of synaptic transmission.

   With further regards to generality, as stated in our Abstract, this paper is concerned with providing a physical theory to describe “rapid and precise neuronal communication” enabled by “a highly synchronous release” of neurotransmitters. Typically, more than 90% of the neurotransmitters are released through synchronous release during the action potential. By applying our theory to each of the multiple Ca!" sensors one will be able to cover the remaining <10% of the neurotransmitters and thus simultaneously describe spontaneous, asynchronous and synchronous release. While detailed studies of these effects are clearly beyond the scope of this work, our theory opens a door for such studies by providing a foundation in the form of a conceptual, analytically tractable framework.

   1. In their derivations, Wang and Dudko collapse the intracellular Ca-concentration [Ca]i, a parameter directly quantified in the several original experiments that went into Fig. 2A, into a dimensionless relative [Ca]i "c" (see equation 7). Similarly, the release rates are collapsed into a dimensionless quantity. With these normalizations, Ca-dependent transmitter release measured in several preparations seems to fall onto a single theoretical prediction (Fig. 2A). The deeper meaning behind the equalization of the data was unclear, except a demonstration that the data from these different experiments can in general be described with a two-pool model, which is at the core of the dimensionless equations. One issue might be that many of the original data sets used here derive from the same preparation (the calyx of Held), and therefore the previous data might not scatter strongly between studies. This could be clarified by the authors by also plotting the data from all studies on the non-normalized [Ca]i axis for comparison. Furthermore, it would be useful to include data from other preparations, like the inner hair cells (Beutner et al. 2001 Neuron; their Fig. 3) which likely have a lower Ca-sensitivity, i.e. are right-shifted as compared to the calyx (see discussion in Woelfel & Schneggenburger 2003 J. Neuroscience). Thus, it is unclear why normalization of [Ca]i to "c" should be an advantage, because differences in the intracellular Ca sensitivity of vesicle fusion exist between synapses (see above), and likely represent important physiological differences between secretory systems.

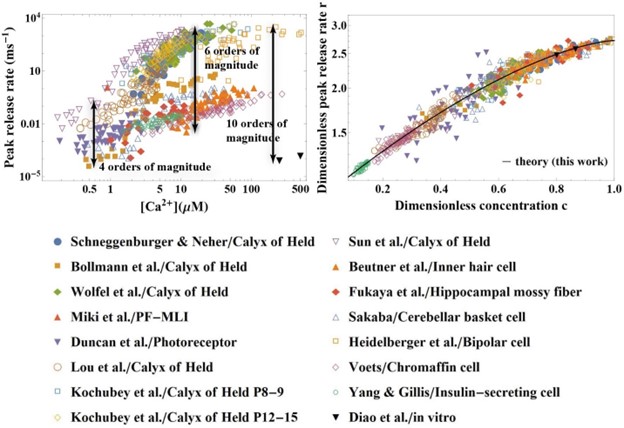
   We thank the Reviewer for challenging our work with the hypothesis that the demonstrated universal scaling of the experimental data could in fact be an artefact caused by pre-selecting the data with the same preparation – addressing this hypothesis is indeed a compelling test to probe the true limits of generality of our theory. Below we carry out this test. We implemented the two suggestions of the Reviewer: (i) we added datasets on markedly different synaptic preparations, including the inner hair cells as suggested by the Reviewer, as well as retina bipolar cell, hippocampal mossy fiber, cerebella basket cell, chromaffin cell, insulin-secreting cell, and additional data on Calyx of Held from multiple laboratories, and (ii) we plotted the data on the non-normalized axis of [Ca2+] to reveal the full extent of scatter among the data sets. The resulting plot (Fig. R1 below) speaks for itself: in vivo data for the release rate span 4 orders of magnitude at low [Ca2+] and 6 orders of magnitude at high [Ca2+], and there is a 10 orders of magnitude difference between the release rates from in vivo and in vitro data. The scatter across 4-10 orders of magnitude allows one to appreciate the vastly different sensitivities to [Ca2+] between synaptic preparations (Fig.R1, left). Yet, all these data collapse beautifully on the master curve established by our theory (Fig.R1, right).

   

   Fig. R1. Despite 10 orders of magnitude variation in the release rate of different synaptic preparations and more than 3 orders of magnitude range of calcium concentration (left), the data collapse onto a universal curve predicted by the theory (right). The universal collapse indicates that the established scaling (Eq. 7) is universal across different synapses. The distinct sets of parameters for individual synapses (Appendix 3 Table 2) is a demonstration of the predictive power of the theory as a tool for extracting the unique properties of each synapse from experimental data.

   What the Reviewer refers to as “the equalization of the data” is known in statistical physics as universality. The deeper meaning of a universal scaling is its indication that the observed phenomena realized in seemingly unrelated systems are in fact governed by common physical principles. The collapse of the data onto the universal curve in Fig. R1 is a demonstration that the present theory has uncovered, quantitatively, unifying physical principles underneath the striking diversity and bewildering complexity of chemical synapses. The Referee is of course correct that the differences in [Ca2+] sensitivities among synapses likely represent important physiological differences between distinct synapses and distinct secretory systems. The present theory does not negate these differences, but it in fact allows one to quantify these differences through the unique sets of extracted parameters for individual synapses (see Appendix 3 Table 2). We are not aware of any other theory that has demonstrated universality in synaptic transmission through a simple, single scaling relation across 10 orders of magnitude in dynamic range and at the same time allowed the extraction of the microscopic parameters that are unique for the individual synapses and thus reflect the diversity of their synaptic machinery. We included Fig. R1 shown here in the revised manuscript (Figure 2).

   1. Finally, the authors use their model to derive the number of SNARE proteins necessary for vesicle fusion, and they arrive at the quite strong conclusion that N = 2 SNAREs are required. Nevertheless, this estimate doesn't fit with the number of n = 4-5 Ca2+ ions which the original studies of Fig. 2A consistently found. The Ca-sensitivity at the calyx of Held, and the steepness of the release rate versus [Ca]i relation is determined by Ca-binding to Synatotagmin-2 (the specific Ca sensor isoform found at the calyx synapse), as has been determined in molecular studies at the calyx synapse (see Sun et al. 2007 Nature; Kochubey & Schneggenburger 2011 Neuron). Furthermore, in other secretory cells, the number of SNARE proteins has been estimated to be {greater than or equal to} 3 (Mohrmann et al., Science 2010).

   The Reviewer is incorrect in their claim that there is any discrepancy here. The number of SNAREs N and the number of Ca2+ ions 𝑄‡ , extracted from the fit to our theory, are actually in a good agreement with the findings from the studies mentioned by the Reviewer. To clarify, the parameter 𝑄‡ is the number of 𝐶𝑎!" ions bound to a SNARE at the transition state (not final state) of the free energy landscape of a SNARE complex. Appendix 3 Table 2 shows that, for all synaptic preparations, the extracted values at the transition state are 𝑄‡ < 4 − 5, which is indeed consistent with n = 4 − 5 at the final state. We note that, in addition, our theory enables one to extract the key energetic parameter that governs synaptic vesicle fusion: the activation free energy barrier ∆𝐺‡ of SNARE conformational transition (in the range 8-34 kBT for different synaptic preparations, see Appendix 3 Table 2), which, to our knowledge, has not been possible to extract from these experiments before.

   The specific value N=2 was extracted from a particular data set for Calyx of Held (Woelfel et al 2007), for which the temporal curves of cumulative release at different Ca2+ concentrations were available. It is quite possible that the value of N will be different for some other synapses. As we emphasize in the manuscript (see Discussion), the present theory does not declare the same value of N for all types of synapses; the power of the theory lies in providing a fitting tool for extracting this value for a system of interest.

   Taken together, the derivation of the analytical equations for the kinetic scheme of a 2-pool model is mathematically interesting, and the scholarly derived equations are trustworthy. Nevertheless, the derived analytical model in fact captures only a specific stage of synaptic transmission focusing on Ca-dependent fusion of vesicles from two pools at [Ca]i >1 microM. Other important processes and mechanistic components (e.g. spontaneous, asynchronous release, Ca-dependent pool replenishment, postsynaptic factors) are either over-simplified or remained out of the scope of the theory. Therefore, the paper is far from providing a general "theory for synaptic transmission", as the title promises.

   We appreciate that the Reviewer sees our analytical derivations as being mathematically interesting, scholarly derived, and trustworthy. We believe that we have convincingly refuted the Reviewer’s criticisms regarding perceived limitations. We have shown that our universal scaling and collapse is not limited to high calcium concentrations, and have presented checks using data from vastly different synaptic preparations. As noted above, the generality of a theory is determined not by the amount of details packed in it but by the ability of the theory to reproduce observations and generate predictions regarding the phenomenon of interest (here: rapid and precise neuronal communication) while containing as few details as possible. Our theory accomplishes just that; it delivers precisely what our title promises.

   Reviewer #2 (Public Review):

   The present MS describes an effort to create a general mathematical model of synaptic neurotransmission. The authors invested great efforts to create a complex model of the presynaptic mechanisms, but their approach of the postsynaptic mechanisms is way oversimplified. The authors claim that their model is consistent with lots of in vivo and in vitro experimental data, but this night be true for a small subselection of experimental papers (they cite 7 experimental papers regularly in the MS!). The authors also indicate that their modeling has a realistic foundation, namely they can relate some parameters in their equations to molecules/molecular mechanisms. One example is the parameter N, which they claim indicate the number of SNARE complexes requires for fusion. The reviewer finds it rather misleading because it alludes that there is a parameter for complexin, Rim1, Rim-BP, Munc13-1 etc... The equations clearly cannot formulate and reflect diversity due to different isoforms of even the above mentioned key presynaptic molecules.

   We appreciate that the Reviewer found 7 different experimental papers – covering different synapses and different experimental setups – to be “a small subselection”. We believe that Fig. R1 above (response to Reviewer #1 point 2), which uses 16 different experimental papers, leaves no further doubts that the claims about the consistency between the theory and data are fully justified. Despite up to 10 orders of magnitude variation in the release rate of different synaptic preparations and more than 3 orders of magnitude range of calcium concentrations (Fig. R1, left), all the data collapse onto a universal curve predicted by our theory (Fig. R1, right). These data represent different systems – from the central nervous system to the secretory system – and come from in vivo and in vitro experiments. The data we have used cover the measurements on all synaptic systems that we could find in the literature on the action potential-driven neurotransmitter release. If the Reviewer is aware of any existing data on other synaptic systems that we might have missed, we will gratefully appreciate the opportunity to apply the theory to those data as well.

   The diversity of the molecular components in different synapses is captured in our theory through different values of the microscopic parameters Δ𝐺‡, 𝑄‡ and 𝑘( . These parameters describe, respectively, the activation energy barrier, the number of bound Ca2+ ions, and the intrinsic rate of the conformational transition of the SNARE complexes that drive synaptic vesicle fusion in a given synapse. Different isoforms of the individual components of SNARE complexes and scaffold proteins, including the proteins mentioned by the Reviewer, will be reflected in different values of Δ𝐺‡, 𝑄‡ and 𝑘( for specific synaptic preparations, as can be seen in Appendix 3 Table 2 in the manuscript. These parameters capture the energetic and kinetic properties of the synaptic fusion machinery as a complex rather than as a collection of isolated molecules. Because the molecular components within a SNARE complex act collectively (hence the name “complex”) to drive vesicle fusion, it is natural (and indeed fortunate) that the predictive power of the theory can be preserved with only a few key parameters of the molecular machinery as opposed to requiring a long list of parameters for every specific isoform of each of the many individual molecular components.

   Read the original source
2. 

   eLife

   May 28, 2022

   Evaluation Summary:

   The present MS describes an effort to create a general mathematical model of synaptic neurotransmission. The authors invested great efforts to create a complex model of the presynaptic mechanisms. This is an exceptionally challenging task and it falls short of a true general theory. Nonetheless, the model will be an important addition to an emerging field attempting to generate predictive models of complex neuronal biophysical processes, including synaptic transmission.

   (This preprint has been reviewed by eLife. We include the public reviews from the reviewers here; the authors also receive private feedback with suggested changes to the manuscript.The reviewers remained anonymous to the authors.)

   Read the original source
3. 

   eLife

   May 28, 2022

   Reviewer #2 (Public Review):

   The present MS describes an effort to create a general mathematical model of synaptic neurotransmission. The authors invested great efforts to create a complex model of the presynaptic mechanisms, but their approach of the postsynaptic mechanisms is way oversimplified. The authors claim that their model is consistent with lots of in vivo and in vitro experimental data, but this night be true for a small subselection of experimental papers (they cite 7 experimental papers regularly in the MS!). The authors also indicate that their modeling has a realistic foundation, namely they can relate some parameters in their equations to molecules/molecular mechanisms. One example is the parameter N, which they claim indicate the number of SNARE complexes requires for fusion. The reviewer finds it rather misleading …

   Reviewer #2 (Public Review):

   The present MS describes an effort to create a general mathematical model of synaptic neurotransmission. The authors invested great efforts to create a complex model of the presynaptic mechanisms, but their approach of the postsynaptic mechanisms is way oversimplified. The authors claim that their model is consistent with lots of in vivo and in vitro experimental data, but this night be true for a small subselection of experimental papers (they cite 7 experimental papers regularly in the MS!). The authors also indicate that their modeling has a realistic foundation, namely they can relate some parameters in their equations to molecules/molecular mechanisms. One example is the parameter N, which they claim indicate the number of SNARE complexes requires for fusion. The reviewer finds it rather misleading because it alludes that there is a parameter for complexin, Rim1, Rim-BP, Munc13-1 etc... The equations clearly cannot formulate and reflect diversity due to different isoforms of even the above mentioned key presynaptic molecules.

   Read the original source
4. 

   eLife

   May 28, 2022

   Reviewer #1 (Public Review):

   Wang and Dudko derive analytical equations for one special case of a model of Ca-dependent vesicle fusion, in the attempt to find a "general theory" of synaptic transmission. They use a model with 2 kinetically distinct fast and slow pools (equation 1).

   Critique

   1. Overall, the analytical approach applied here remains limited to the quite arbitrarily chosen 2-pool model. Thus, while the authors are able to re-capitulate the kinetics of transmitter release under a series of defined intracellular Ca-concentration steps, [Ca]i (see Fig. 2B; data from Woelfel et al. 2007 J. Neuroscience), this is nevertheless not surprising because the data by Woelfel et al. was originally also fit with a 2-pool model. More importantly, the 2-pool model is valid for describing release kinetics at high [Ca]i, but it cannot account …

   Reviewer #1 (Public Review):

   Wang and Dudko derive analytical equations for one special case of a model of Ca-dependent vesicle fusion, in the attempt to find a "general theory" of synaptic transmission. They use a model with 2 kinetically distinct fast and slow pools (equation 1).

   Critique

   1. Overall, the analytical approach applied here remains limited to the quite arbitrarily chosen 2-pool model. Thus, while the authors are able to re-capitulate the kinetics of transmitter release under a series of defined intracellular Ca-concentration steps, [Ca]i (see Fig. 2B; data from Woelfel et al. 2007 J. Neuroscience), this is nevertheless not surprising because the data by Woelfel et al. was originally also fit with a 2-pool model. More importantly, the 2-pool model is valid for describing release kinetics at high [Ca]i, but it cannot account for other important phenomena of synaptic transmission like e.g. spontaneous and asynchronous release which happen at lower [Ca]i, with different Ca cooperativity (Lou et al., 2005). Along the same lines, the derivations of the equations by Wang and Dudko are not valid in the range of low [Ca]i below about 1 micromolar (see "private recommendations" for details). This, however, limits the applicability of the model to AP-driven transmitter release, and it shows that based on one specific arbitrarily chosen model (here: the 2-pool model), one cannot claim to build a realistic and full "theory" for synaptic transmission.

   2. In their derivations, Wang and Dudko collapse the intracellular Ca-concentration [Ca]i, a parameter directly quantified in the several original experiments that went into Fig. 2A, into a dimensionless relative [Ca]i "c" (see equation 7). Similarly, the release rates are collapsed into a dimensionless quantity. With these normalizations, Ca-dependent transmitter release measured in several preparations seems to fall onto a single theoretical prediction (Fig. 2A). The deeper meaning behind the equalization of the data was unclear, except a demonstration that the data from these different experiments can in general be described with a two-pool model, which is at the core of the dimensionless equations. One issue might be that many of the original data sets used here derive from the same preparation (the calyx of Held), and therefore the previous data might not scatter strongly between studies. This could be clarified by the authors by also plotting the data from all studies on the non-normalized [Ca]i axis for comparison. Furthermore, it would be useful to include data from other preparations, like the inner hair cells (Beutner et al. 2001 Neuron; their Fig. 3) which likely have a lower Ca-sensitivity, i.e. are right-shifted as compared to the calyx (see discussion in Woelfel & Schneggenburger 2003 J. Neuroscience). Thus, it is unclear why normalization of [Ca]i to "c" should be an advantage, because differences in the intracellular Ca sensitivity of vesicle fusion exist between synapses (see above), and likely represent important physiological differences between secretory systems.

   3. Finally, the authors use their model to derive the number of SNARE proteins necessary for vesicle fusion, and they arrive at the quite strong conclusion that N = 2 SNAREs are required. Nevertheless, this estimate doesn't fit with the number of n = 4-5 Ca2+ ions which the original studies of Fig. 2A consistently found. The Ca-sensitivity at the calyx of Held, and the steepness of the release rate versus [Ca]i relation is determined by Ca-binding to Synatotagmin-2 (the specific Ca sensor isoform found at the calyx synapse), as has been determined in molecular studies at the calyx synapse (see Sun et al. 2007 Nature; Kochubey & Schneggenburger 2011 Neuron). Furthermore, in other secretory cells, the number of SNARE proteins has been estimated to be {greater than or equal to} 3 (Mohrmann et al., Science 2010).

   Taken together, the derivation of the analytical equations for the kinetic scheme of a 2-pool model is mathematically interesting, and the scholarly derived equations are trustworthy. Nevertheless, the derived analytical model in fact captures only a specific stage of synaptic transmission focusing on Ca-dependent fusion of vesicles from two pools at [Ca]i >1 microM. Other important processes and mechanistic components (e.g. spontaneous, asynchronous release, Ca-dependent pool replenishment, postsynaptic factors) are either over-simplified or remained out of the scope of the theory. Therefore, the paper is far from providing a general "theory for synaptic transmission", as the title promises.

   Read the original source
5. 

   Version published to 10.7554/elife.73585 on eLife

   Dec 31, 2021
6. 

   Version published to 10.1101/2020.12.17.423159v2 on bioRxiv

   Jan 30, 2021
7. 

   Version published to 10.1101/2020.12.17.423159v1 on bioRxiv

   Dec 19, 2020