Resonating neurons stabilize heterogeneous grid-cell networks

Article activity feed

1. 

   Version published to 10.7554/elife.66804 on eLife

   Jul 30, 2021
2. 

   eLife

   Jul 26, 2021

   Author Response:

   We thank the editors and the reviewers for their careful reading and rigorous evaluation of our manuscript. We thank them for their positive comments and constructive feedback, which led us to add further lines of evidence in support of our central hypothesis that intrinsic neuronal resonance could stabilize heterogeneous grid-cell networks through targeted suppression of low-frequency perturbations. In the revised manuscript, we have added a physiologically rooted mechanistic model for intrinsic neuronal resonance, introduced through a slow negative feedback loop. We show that stabilization of patterned neural activity in a heterogeneous continuous attractor network (CAN) model could be achieved with this resonating neuronal model. These new results establish the generality of the stabilizing role of neuronal resonance …

   Author Response:

   We thank the editors and the reviewers for their careful reading and rigorous evaluation of our manuscript. We thank them for their positive comments and constructive feedback, which led us to add further lines of evidence in support of our central hypothesis that intrinsic neuronal resonance could stabilize heterogeneous grid-cell networks through targeted suppression of low-frequency perturbations. In the revised manuscript, we have added a physiologically rooted mechanistic model for intrinsic neuronal resonance, introduced through a slow negative feedback loop. We show that stabilization of patterned neural activity in a heterogeneous continuous attractor network (CAN) model could be achieved with this resonating neuronal model. These new results establish the generality of the stabilizing role of neuronal resonance in a manner independent of how resonance was introduced. More importantly, by specifically manipulating the feedback time constant in the neural dynamics, we establish the critical role of the slow kinetics of the negative feedback loop in stabilizing network function. These results provide additional direct lines of evidence for our hypothesis on the stabilizing role of resonance in the CAN model employed here. Intuitively, we envisage intrinsic neuronal resonance as a specific cellular-scale instance of a negative feedback loop. The negative feedback loop is a well-established network motif that acts as a stabilizing agent and suppresses the impact of internal and external perturbations in engineering applications and biological networks.

   Reviewer #1 (Public Review):

   The authors succeed in conveying a clear and concise description of how intrinsic heterogeneity affects continuous attractor models. The main claim, namely that resonant neurons could stabilize grid-cell patterns in medial entorhinal cortex, is striking.

   We thank the reviewer for their time and effort in evaluating our manuscript, and for their rigorous evaluation and positive comments on our study.

   I am intrigued by the use of a nonlinear filter composed of the product of s with its temporal derivative raised to an exponent. Why this particular choice? Or, to be more specific, would a linear bandpass filter not have served the same purpose?

   Please note that the exponent was merely a mechanism to effectively tune the resonance frequency of the resonating neuron. In the revised manuscript, we have introduced a new physiologically rooted means to introduce intrinsic neuronal resonance, thereby confirming that network stabilization achieved was independent of the formulation employed to achieve resonance.

   The magnitude spectra are subtracted and then normalized by a sum. I have slight misgivings about the normalization, but I am more worried that, as no specific formula is given, some MATLAB function has been used. What bothers me a bit is that, depending on how the spectrogram/periodogram is computed (in particular, averaged over windows), one would naturally expect lower frequency components to be more variable. But this excess variability at low frequencies is a major point in the paper.

   We have now provided the specific formula employed for normalization as equation (16) of the revised manuscript. We have also noted that this was performed to account for potential differences in the maximum value of the homogeneous vs. heterogeneous spectra. The details are provided in the Methods subsection “Quantitative analysis of grid cell temporal activity in the spectral domain” of the revised manuscript. Please note that what is computed is the spectra of the entire activity pattern, and not a periodogram or a scalogram. There was no tiling of the time-frequency plane involved, thus eliminating potential roles of variables there on the computation here.

   In addition to using variances of normalized differences to quantify spectral distributions, we have also independently employed octave-based analyses (which doesn’t involve normalized differences) to strengthen our claims about the impact of heterogeneities and resonance on different bands of frequency. These octave-based analyses also confirm our conclusions on the impact of heterogeneities and neuronal resonance on low-frequency components.

   Finally, we would like to emphasize that spectral computations are the same for different networks, with networks designed in such a way that there was only one component that was different. For instance, in introducing heterogeneities, all other parameters of the network (the specific trajectory, the seed values, the neural and network parameters, the connectivity, etc.) remained exactly the same with the only difference introduced being confined to the heterogeneities. Computation of the spectral properties followed identical procedures with activity from individual neurons in the two networks, and comparison was with reference to identically placed neurons in the two networks. Together, based on the several routes to quantifying spectral signatures, based on the experimental design involved, and based on the absence of any signal-specific tiling of the time-frequency plane, we argue that the impact of heterogeneities or the resonators on low-frequency components is not an artifact of the analysis procedures.

   We thank the reviewer for raising this issue, as it helped us to elaborate on the analysis procedures employed in our study.

   Which brings me to the main thesis of the manuscript: given the observation of how heterogeneities increase the variability in the low temporal frequency components, the way resonant neurons stabilize grid patterns is by suppressing these same low frequency components.

   I am not entirely convinced that the observed correlation implies causality. The low temporal frequeny spectra are an indirect reflection of the regularity or irregularity of the pattern formation on the network, induced by the fact that there is velocity coupling to the input and hence dynamics on the network. Heterogeneities will distort the pattern on the network, that is true, but it isn't clear how introducing a bandpass property in temporal frequency space affects spatial stability causally.

   Put it this way: imagine all neurons were true oscillators, only capable of oscillating at 8 Hz. If they were to synchronize within a bump, one will have the field blinking on and off. Nothing wrong with that, and it might be that such oscillatory pattern formation on the network might be more stable than non-oscillatory pattern formation (perhaps one could even demonstrate this mathematically, for equivalent parameter settings), but this kind of causality is not what is shown in the manuscript.

   The central hypothesis of our study was that intrinsic neuronal resonance could stabilize heterogeneous grid-cell networksthrough targeted suppression of low-frequency perturbations.

   In the revised manuscript, we present the following lines of evidence in support of this hypothesis (mentioned now in the first paragraph of the discussion section of the revised manuscript):

   1. Neural-circuit heterogeneities destabilized grid-patterned activity generation in a 2D CAN model (Figures 2–3).

   2. Neural-circuit heterogeneities predominantly introduced perturbations in the lowfrequency components of neural activity (Figure 4).

   3. Targeted suppression of low-frequency components through phenomenological (Figure 5C) or through mechanistic (new Figure 9D) resonators resulted in stabilization of the heterogeneous CAN models (Figure 8 and new Figure 11). We note that the stabilization was achieved irrespective of the means employed to suppress low-frequency components: an activity-independent suppression of low-frequencies (Figure 5) or an activity-dependent slow negative feedback loop (new Figure 9).

   4. Changing the feedback time constant τm in mechanistic resonators, without changes to neural gain or the feedback strength allowed us to control the specific range of frequencies that would be suppressed. Our analyses showed that a slow negative feedback loop, which results in targeted suppression of low-frequency components, was essential in stabilizing grid-patterned activity (new Figure 12). As the slow negative feedback loop and the resultant suppression of low frequencies mediates intrinsic resonance, these analyses provide important lines of evidence for the role of targeted suppression of low frequencies in stabilizing grid patterned activity.

   5. We demonstrate that the incorporation of phenomenological (Figure 13A–C) or mechanistic (new Figure panels 13D–F) resonators specifically suppressed lower frequencies of activity in the 2D CAN model.

   6. Finally, the incorporation of resonance through a negative feedback loop allowed us to link our analyses to the well-established role of network motifs involving negative feedback loops in inducing stability and suppressing external/internal noise in engineering and biological systems. We envisage intrinsic neuronal resonance as a cellular-scale activitydependent negative feedback mechanism, a specific instance of a well-established network motif that effectuates stability and suppresses perturbations across different networks (Savageau, 1974; Becskei and Serrano, 2000; Thattai and van Oudenaarden, 2001; Austin et al., 2006; Dublanche et al., 2006; Raj and van Oudenaarden, 2008; Lestas et al., 2010; Cheong et al., 2011; Voliotis et al., 2014). A detailed discussion on this important link to the stabilizing role of this network motif, with appropriate references to the literature is included in the new discussion subsection “Slow negative feedback: Stability, noise suppression, and robustness”.

   We thank the reviewer for their detailed comments. These comments helped us to introducing a more physiologically rooted mechanistic form of resonance, where we were able to assess the impact of slow kinetics of negative feedback on network stability, thereby providing more direct lines of evidence for our hypothesis. This also allowed us to link resonance to the wellestablished stability motif: the negative feedback loop. We also note that our analyses don’t employ resonance as a route to introducing oscillations in the network, but as a means for targeted suppression of low-frequency perturbations through a negative feedback loop. Given the strong quantitative links of negative feedback loops to introducing stability and suppressing the impact of perturbations in engineering applications and biological networks, we envisage intrinsic neuronal resonance as a stability-inducing cellular-scale activity-dependent negative feedback mechanism.

   Reviewer #2 (Public Review):

   [...] The pars construens demonstrates that similar networks, but comprised of units with different dynamical behavior, essentially amputated of their slowest components, do not suffer from the heterogeneities - they still produce grids. This part proceeds through 3 main steps: a) defining "resonator" units as model neurons with amputated low frequencies (Fig. 5); b) showing that inserted into the same homogeneous CAN network, "resonator" units produce the same grids as "integrator" units (Figs. 6,7); c) demonstrating that however the network with "resonator" units is resistant to heterogeneities (Fig. 8). Figs. 9 and 10 help understand what has produced the desired grid stabilization effect. This second part is on the whole also well structured, and its step c) is particularly convincing.

   We thank the reviewer for their time and effort in evaluating our manuscript, and for their rigorous evaluation and positive comments on our study.

   Step b) intends to show that nothing important changes, in grid pattern terms, if one replaces the standard firing rate units with the ad hoc defined units without low frequency behavior. The exact outcome of the manipulation is somewhat complex, as shown in Figs. 6 and 7, but it could be conceivably summed up by stating that grids remain stable, when low frequencies are removed. What is missing, however, is an exploration of whether the newly defined units, the "resonators", could produce grid patterns on their own, without the CAN arising from the interactions between units, just as a single-unit effect. I bet they could, because that is what happens in the adaptation model for the emergence of the grid pattern, which we have studied extensively over the years. Maybe with some changes here and there, but I believe the CAN can be disposed of entirely, except to produce a common alignment between units, as we have shown.

   Step a), finally, is the part of the study that I find certainly not wrong, but somewhat misleading. Not wrong, because what units to use in a model, and what to call them, is a legitimate arbitrary choice of the modelers. Somewhat misleading, because the term "resonator" evokes a more specific dynamical behavior that than obtained by inserting Eqs. (8)-(9) into Eq. (6), which amounts to a brute force amputation of the low frequencies, without any real resonance to speak of. Unsurprisingly, Fig. 5, which is very clear and useful, does not show any resonance, but just a smooth, broad band-pass behavior, which is, I stress legitimately, put there by hand. A very similar broad band-pass would result from incorporating into individual units a model of firing rate adaptation, which is why I believe the "resonator" units in this study would generate grid patterns, in principle, without any CAN.

   We thank the reviewer for these constructive comments and questions, as they were extremely helpful in (i) formulating a new model for rate-based resonating neurons that is more physiologically rooted; (ii) demonstrating the stabilizing role of resonance irrespective of model choices that implemented resonance; and (iii) mechanistically exploring the impact of targeted suppression of low frequency components in neural activity. We answer these comments of the reviewer in two parts, the first addressing other models for grid-patterned activity generation and the second addressing the reviewer’s comment on “brute force amputation of the low frequencies” in the resonator neuron presented in the previous version of our manuscript.

   I. Other models for grid-patterned activity generation.

   In the adaptation model (Kropff and Treves, 2008; Urdapilleta et al., 2017; Stella et al., 2020), adaptation in conjunction with place-cell inputs, Hebbian synaptic plasticity, and intrinsic plasticity (in gain and threshold) to implement competition are together sufficient for the emergence of the grid-patterned neural activity. However, the CAN model that we chose as the substrate for assessing the impact of neural circuit heterogeneities on functional stability is not equipped with the additional components (place-cell inputs, synaptic/intrinsic plasticity). Therefore, we note that decoupling the single unit (resonator or integrator) from the network does not yield grid-patterned activity.

   However, we do agree that a resonator neuron endowed with additional components from the adaptation model would be sufficient to elicit grid-patterned neural activity. This is especially clear with the newly introduced mechanistic model for resonance through a slow feedback loop (Figure 9). Specifically, resonating conductances such as HCN and M-type potassium channels can effectuate spike-frequency adaptation. One of the prominent channels that is implicated in introducing adaptation, the calcium-activated potassium channels implement a slow activitydependent negative feedback loop through the slow calcium kinetics. Neural activity drives calcium influx, and the slow kinetics of the calcium along with the channel-activation kinetics drive a potassium current that completes a negative feedback loop that inhibits neural activity. Consistently, one of the earliest-reported forms of electrical resonance in cochlear hair cells was shown to be mediated by calcium-activated potassium channels (Crawford and Fettiplace, 1978, 1981; Fettiplace and Fuchs, 1999). Thus, adaptation realized as a slow negative-feedback loop, in conjunction with place-cell inputs and intrinsic/synaptic plasticity would elicit gridpatterned neural activity as demonstrated earlier (Kropff and Treves, 2008; Urdapilleta et al., 2017; Stella et al., 2020).

   There are several models for the emergence of grid-patterned activity, and resonance plays distinct roles (compared to the role proposed through our analyses) in some of these models (Giocomo et al., 2007; Kropff and Treves, 2008; Burak and Fiete, 2009; Burgess and O'Keefe, 2011; Giocomo et al., 2011b; Giocomo et al., 2011a; Navratilova et al., 2012; Pastoll et al., 2012; Couey et al., 2013; Domnisoru et al., 2013; Schmidt-Hieber and Hausser, 2013; Yoon et al., 2013; Schmidt-Hieber et al., 2017; Urdapilleta et al., 2017; Stella et al., 2020; Tukker et al., 2021). However, a common caveat that spans many of these models is that they assume homogeneous networks that do not account for the ubiquitous heterogeneities that span neural circuits. Our goal in this study was to take a step towards rectifying this caveat, towards understanding the impact of neural circuit heterogeneities on network stability. We chose the 2D CAN model for grid-patterned activity generation as the substrate for addressing this important yet under-explored question on the role of biological heterogeneities on network function. As we have mentioned in the discussion section, this choice implies that our conclusions are limited to the 2D CAN model for grid patterned generation; these conclusions cannot be extrapolated to other networks or other models for grid-patterned activity generation without detailed analyses of the impact of neural circuit heterogeneities in those models. As our focus here was on the stabilizing role of resonance in heterogeneous neural networks, with 2D CAN model as the substrate, we have not implemented the other models for grid-patterned generation. The impact of biological heterogeneities and resonance on each of these models should be independently addressed with systematic analyses similar to our analyses for the 2D CAN model. As different models for grid-patterned activity generation are endowed with disparate dynamics, and have different roles for resonance, it is conceivable that the impact of biological heterogeneities and intrinsic neuronal resonance have differential impact on these different models. We have mentioned this as a clear limitation of our analyses in the discussion section, also presenting future directions for associated analyses(subsection: “Future directions and considerations in model interpretation”).

   II. Brute force amputation of the low frequencies in the resonator model.

   We completely agree with the reviewer on the observation that the resonator model employed in the previous version of our manuscript was rather artificial, with the realization involving brute force amputation of the lower frequencies. To address this concern, in the revised manuscript, we constructed a new mechanistic model for single-neuron resonance that matches the dynamical behavior of physiological resonators. Specifically, we noted that physiological resonance is elicited by a slow activity-dependent negative feedback (Hutcheon and Yarom, 2000). To incorporate resonance into our rate-based model neurons, we mimicked this by introducing a slow negative feedback loop into our single-neuron dynamics (the motivations are elaborated in the new results subsection “Mechanistic model of neuronal intrinsic resonance: Incorporating a slow activity-dependent negative feedback loop”). The singleneuron dynamics of mechanistic resonators were defined as follows:

   

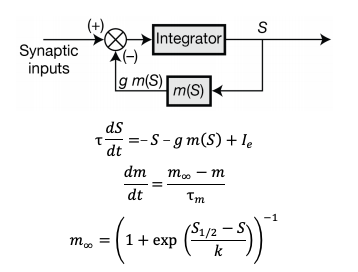
   Here, S governed neuronal activity, τ defined the feedback state variable, g represented the integration time constant, Ie was the external current, and g represented feedback strength. The slow kinetics of the negative feedback was controlled by the feedback time constant (τm). In order to manifest resonance, τm > τ (Hutcheon and Yarom, 2000). The steady-state feedback kernel (m∞) of the negative feedback is sigmoidally dependent on the output of the neuron (S), defined by two parameters: half-maximal activity (S1/2) and slope (k). The single-neuron dynamics are elaborated in detail in the methods section (new subsection: Mechanistic model for introducing intrinsic resonance in rate-based neurons).

   We first demonstrate that the introduction of a slow-negative feedback loop introduce resonance into single-neuron dynamics (new Figure 9D–E). We performed systematic sensitivity analyses associated with the parameters of the feedback loop and characterized the dependencies of intrinsic neuronal resonance on model parameters (new Figure 9F–I). We demonstrate that the incorporation of resonance through a negative feedback loop was able to generate grid-patterned activity in the 2D CAN model employed here, with clear dependencies on model parameters (new Figure 10; new Figure 10-Supplements1–2). Next, we incorporated heterogeneities into the network and demonstrated that the introduction of resonance through a negative feedback loop stabilized grid-patterned generation in the heterogeneous 2D CAN model (new Figure 11).

   The mechanistic route to introducing resonance allowed us to probe the basis for the stabilization of grid-patterned activity more thoroughly. Specifically, with physiological resonators, resonance manifests only when the feedback loop is slow (new Figure 9I; Hutcheon and Yarom, 2000). This allowed us an additional mechanistic handle to directly probe the role of resonance in stabilizing the grid patterned activity. We assessed the emergence of grid-patterned activity in heterogeneous CAN models constructed with networks constructors with neurons with different τm values (new Figure 12). Strikingly, we found that when τm value was small (resulting in fast feedback loops), there was no stabilization of gridpatterned activity in the CAN model, especially with the highest degree of heterogeneities (new Figure 12). With progressive increase in τm, the patterns stabilized with grid score increasing with τm=25 ms (new Figure 12) and beyond (new Figure 11B; τm=75 ms). Finally, our spectral analyses comparing frequency components of homogeneous vs. heterogeneous resonator networks (new Figure panels 13D–F) showed the suppression of low-frequency perturbations in heterogeneous CAN networks.

   We gratefully thank the reviewer for raising the issue with the phenomenological resonator model. This allowed us to design the new resonator model and provide several new lines of evidence in support of our central hypothesis. The incorporation of resonance through a negative feedback loop also allowed us to link our analyses to the well-established role of network motifs involving negative feedback loops in inducing stability and suppressing external/internal noise in engineering and biological systems. We envisage intrinsic neuronal resonance as a cellular-scale activity-dependent negative feedback mechanism, a specific instance of a well-established network motif that effectuates stability and suppresses perturbations across different networks (Savageau, 1974; Becskei and Serrano, 2000; Thattai and van Oudenaarden, 2001; Austin et al., 2006; Dublanche et al., 2006; Raj and van Oudenaarden, 2008; Lestas et al., 2010; Cheong et al., 2011; Voliotis et al., 2014). A detailed discussion on this important link to the stabilizing role of this network motif, with appropriate references to the literature is included in the new discussion subsection “Slow negative feedback: Stability, noise suppression, and robustness”.

   Read the original source
3. 

   eLife

   Jul 26, 2021

   Evaluation Summary:

   This is a careful and systematic simulation study that convincingly illustrates a role for intrinsic resonance properties in suppressing the effects of cellular and network heterogeneities in a continuous attractor network model of grid cell firing patterns. The study shows that overly simplified models of neurons can lead to fragility in important network level behaviour and that intrinsic neuronal properties strongly influence relevant network level dynamics. This an important result that likely applies to a broad range of network models. Further investigation into the mechanism, possibly using a simplified model, would substantiate the simulation results and fully exploit the power of models in providing intuition and illustrating the generality of the observations.

   (This preprint has been reviewed by eLife. We …

   Evaluation Summary:

   This is a careful and systematic simulation study that convincingly illustrates a role for intrinsic resonance properties in suppressing the effects of cellular and network heterogeneities in a continuous attractor network model of grid cell firing patterns. The study shows that overly simplified models of neurons can lead to fragility in important network level behaviour and that intrinsic neuronal properties strongly influence relevant network level dynamics. This an important result that likely applies to a broad range of network models. Further investigation into the mechanism, possibly using a simplified model, would substantiate the simulation results and fully exploit the power of models in providing intuition and illustrating the generality of the observations.

   (This preprint has been reviewed by eLife. We include the public reviews from the reviewers here; the authors also receive private feedback with suggested changes to the manuscript. Reviewer #2 agreed to share their name with the authors.)

   Read the original source
4. 

   eLife

   Jul 26, 2021

   Reviewer #1 (Public Review):

   The authors succeed in conveying a clear and concise description of how intrinsic heterogeneity affects continuous attractor models. The main claim, namely that resonant neurons could stabilize grid-cell patterns in medial entorhinal cortex, is striking.

   I am intrigued by the use of a nonlinear filter composed of the product of s with its temporal derivative raised to an exponent. Why this particular choice? Or, to be more specific, would a linear bandpass filter not have served the same purpose?

   The magnitude spectra are subtracted and then normalized by a sum. I have slight misgivings about the normalization, but I am more worried that , as no specific formula is given, some MATLAB function has been used. What bothers me a bit is that, depending on how the spectrogram/periodogram is computed (in …

   Reviewer #1 (Public Review):

   The authors succeed in conveying a clear and concise description of how intrinsic heterogeneity affects continuous attractor models. The main claim, namely that resonant neurons could stabilize grid-cell patterns in medial entorhinal cortex, is striking.

   I am intrigued by the use of a nonlinear filter composed of the product of s with its temporal derivative raised to an exponent. Why this particular choice? Or, to be more specific, would a linear bandpass filter not have served the same purpose?

   The magnitude spectra are subtracted and then normalized by a sum. I have slight misgivings about the normalization, but I am more worried that , as no specific formula is given, some MATLAB function has been used. What bothers me a bit is that, depending on how the spectrogram/periodogram is computed (in particular, averaged over windows), one would naturally expect lower frequency components to be more variable. But this excess variability at low frequencies is a major point in the paper.

   Which brings me to the main thesis of the manuscript: given the observation of how heterogeneities increase the variability in the low temporal frequency components, the way resonant neurons stabilize grid patterns is by suppressing these same low frequency components.

   I am not entirely convinced that the observed correlation implies causality. The low temporal frequeny spectra are an indirect reflection of the regularity or irregularity of the pattern formation on the network, induced by the fact that there is velocity coupling to the input and hence dynamics on the network. Heterogeneities will distort the pattern on the network, that is true, but it isn't clear how introducing a bandpass property in temporal frequency space affects spatial stability causally.

   Put it this way: imagine all neurons were true oscillators, only capable of oscillating at 8 Hz. If they were to synchronize within a bump, one will have the field blinking on and off. Nothing wrong with that, and it might be that such oscillatory pattern formation on the network might be more stable than non-oscillatory pattern formation (perhaps one could even demonstrate this mathematically, for equivalent parameter settings), but this kind of causality is not what is shown in the manuscript.

   Read the original source
5. 

   eLife

   Jul 26, 2021

   Reviewer #2 (Public Review):

   The manuscript takes a remarkably systematic and unbiased approach to the question of whether the models, that explain in terms of recurrent connectivity the grid firing patterns observed in the entorhinal cortex of rodents and other species, would really work given heterogeneity in the values of several parameters, that in the standard models are assumed to take a fixed value. Since the real degree of heterogeneity is difficult to measure, but even more because it is difficult to relate measured quantities to the parameters in simple models which perforce include many artificial components, the authors proceed by setting 5 levels of heterogeneity in 3 parameters, and by simulating the network with each parameter made heterogeneous alone, or all 3 in combination. In short, grids are destabilized (Figure 2), …

   Reviewer #2 (Public Review):

   The manuscript takes a remarkably systematic and unbiased approach to the question of whether the models, that explain in terms of recurrent connectivity the grid firing patterns observed in the entorhinal cortex of rodents and other species, would really work given heterogeneity in the values of several parameters, that in the standard models are assumed to take a fixed value. Since the real degree of heterogeneity is difficult to measure, but even more because it is difficult to relate measured quantities to the parameters in simple models which perforce include many artificial components, the authors proceed by setting 5 levels of heterogeneity in 3 parameters, and by simulating the network with each parameter made heterogeneous alone, or all 3 in combination. In short, grids are destabilized (Figure 2), but with interesting differential effects on different aspects of the activity patterns (Fig. 3). This pars destruens is clear, strong and entirely convincing. It is concluded by showing that heterogeneities act on the slow components of the dynamics (Fig. 4).

   The pars construens demonstrates that similar networks, but comprised of units with different dynamical behavior, essentially amputated of their slowest components, do not suffer from the heterogeneities - they still produce grids. This part proceeds through 3 main steps: a) defining "resonator" units as model neurons with amputated low frequencies (Fig. 5); b) showing that inserted into the same homogeneous CAN network, "resonator" units produce the same grids as "integrator" units (Figs. 6,7); c) demonstrating that however the network with "resonator" units is resistant to heterogeneities (Fig. 8). Figs. 9 and 10 help understand what has produced the desired grid stabilization effect. This second part is on the whole also well structured, and its step c) is particularly convincing.

   Step b) intends to show that nothing important changes, in grid pattern terms, if one replaces the standard firing rate units with the ad hoc defined units without low frequency behavior. The exact outcome of the manipulation is somewhat complex, as shown in Figs. 6 and 7, but it could be conceivably summed up by stating that grids remain stable, when low frequencies are removed. What is missing, however, is an exploration of whether the newly defined units, the "resonators", could produce grid patterns on their own, without the CAN arising from the interactions between units, just as a single-unit effect. I bet they could, because that is what happens in the adaptation model for the emergence of the grid pattern, which we have studied extensively over the years. Maybe with some changes here and there, but I believe the CAN can be disposed of entirely, except to produce a common alignment between units, as we have shown.

   Step a), finally, is the part of the study that I find certainly not wrong, but somewhat misleading. Not wrong, because what units to use in a model, and what to call them, is a legitimate arbitrary choice of the modelers. Somewhat misleading, because the term "resonator" evokes a more specific dynamical behavior that than obtained by inserting Eqs. (8)-(9) into Eq. (6), which amounts to a brute force amputation of the low frequencies, without any real resonance to speak of. Unsurprisingly, Fig. 5, which is very clear and useful, does not show any resonance, but just a smooth, broad band-pass behavior, which is, I stress legitimately, put there by hand. A very similar broad band-pass would result from incorporating into individual units a model of firing rate adaptation, which is why I believe the "resonator" units in this study would generate grid patterns, in principle, without any CAN.

   Read the original source
6. 

   Version published to 10.1101/2020.12.10.419200v2 on bioRxiv

   Jul 20, 2021
7. 

   Version published to 10.1101/2020.12.10.419200v1 on bioRxiv

   Dec 11, 2020