The cellular architecture of memory modules in Drosophila supports stochastic input integration
Curation statements for this article:-
Curated by eLife
eLife assessment
Detailed electron-microscopy reconstructions of neurons, which are now available for a complete Drosophila central brain, raise the prospect of detailed models of their electrical properties. This manuscript uses a recently released dataset to model one particular neuron in an olfactory learning center of the fly brain. The model elucidates how this neuron responds to synaptic inputs that represent odor, suggesting how modification of these synapses might underlie olfactory memory. This work brings together electrophysiological recordings and neuroanatomical reconstructions from volume electron microscopy to model how a neuronal arbor integrates synaptic inputs. With the many ongoing connectome mapping projects world wide, the results here can illustrate an approach to interpretation of connectomes towards understanding neural circuit function. The rules of synaptic plasticity discussed here furthermore do not only shed light into the mechanisms of learning and memory in biological systems but also inspire the formulation of new approaches to adjusting connection weights in artificial neural networks.
This article has been Reviewed by the following groups
Discuss this preprint
Start a discussion What are Sciety discussions?Listed in
- Evaluated articles (eLife)
Abstract
The ability to associate neutral stimuli with valence information and to store these associations as memories forms the basis for decision making. To determine the underlying computational principles, we build a realistic computational model of a central decision module within the Drosophila mushroom body (MB), the fly’s center for learning and memory. Our model combines the electron microscopy-based architecture of one MB output neuron (MBON-α3), the synaptic connectivity of its 948 presynaptic Kenyon cells (KCs), and its membrane properties obtained from patch-clamp recordings. We show that this neuron is electrotonically compact and that synaptic input corresponding to simulated odor input robustly drives its spiking behavior. Therefore, sparse innervation by KCs can efficiently control and modulate MBON activity in response to learning with minimal requirements on the specificity of synaptic localization. This architecture allows efficient storage of large numbers of memories using the flexible stochastic connectivity of the circuit.
Article activity feed
-

-

Author Response
Reviewer #2 (Public Review):
"The cellular architecture of memory modules in Drosophila supports stochastic input integration" is a classical biophysical compartmental modelling study. It takes advantage of some simple current injection protocols in a massively complex mushroom body neuron called MBON-a3 and compartmental models that simulate the electrophysiological behaviour given a detailed description of the anatomical extent of its neurites.
This work is interesting in a number of ways:
- The input structure information comes from EM data (Kenyon cells) although this is not discussed much in the paper - The paper predicts a potentially novel normalization of the throughput of KC inputs at the level of the proximal dendrite and soma - It claims a new computational principle in dendrites, this didn’t become very …
Author Response
Reviewer #2 (Public Review):
"The cellular architecture of memory modules in Drosophila supports stochastic input integration" is a classical biophysical compartmental modelling study. It takes advantage of some simple current injection protocols in a massively complex mushroom body neuron called MBON-a3 and compartmental models that simulate the electrophysiological behaviour given a detailed description of the anatomical extent of its neurites.
This work is interesting in a number of ways:
- The input structure information comes from EM data (Kenyon cells) although this is not discussed much in the paper - The paper predicts a potentially novel normalization of the throughput of KC inputs at the level of the proximal dendrite and soma - It claims a new computational principle in dendrites, this didn’t become very clear to me Problems I see:
- The current injections did not last long enough to reach steady state (e.g. Figure 1FG), and the model current injection traces have two time constants but the data only one (Figure 2DF). This does not make me very confident in the results and conclusions.
These are two important but separate questions that we would like to address in turn.
As for the first, in our new recordings using cytoplasmic GFP to identify MBON-alpha3, we performed both a 200 ms current injection and performed prolonged recordings of 400 ms to reach steady state (for all 4 new cells 1’-4’). For comparison with the original dataset we mainly present the raw traces for 200 ms recordings in Figure 1 Supplement 2. In addition, we now provide a direct comparison of these recordings (200 ms versus 400 ms) and did not observe significant differences in tau between these data (Figure 1 Supplement 2 K). This comparison illustrates that the 200 ms current injection reaches a maximum voltage deflection that is close to the steady state level of the prolonged protocol. Importantly, the critical parameter (tau) did not change between these datasets.
Regarding the second question, the two different time constants, we thank the reviewer for pointing this out. Indeed, while the simulated voltage follows an approximately exponential decay which is, by design, essentially identical to the measured value (τ≈ 16ms, from Table 1; ee Figure 1 Supplement 2 for details), the voltage decays and rises much faster immediately following the onset and offset of the current injections. We believe that this is due to the morphology of this neuron. Current injection, and voltage recordings, are at the soma which is connected to the remainder of the neuron by a long and thin neurite. This ’remainder’ is, of course, in linear size, volume and surface (membrane) area much larger than the soma, see Fig 2A. As a result, a current injection will first quickly charge up the membrane of the soma, resulting in the initial fast voltage changes seen in Fig 2D,F, before the membrane in the remainder of the cell is charged, with the cell’s time constant τ.
We confirmed this intuition by running various simplified simulations in Neuron which indeed show a much more rapid change at step changes in injected current than over the long-term. Indeed, we found that the pattern even appears in the simplest possible two-compartment version of the neuron’s equivalent circuit which we solved in an all-purpose numerical simulator of electrical circuitry (https://www.falstad.com/circuit). The circuit is shown in Figure 1. We chose rather generic values for the circuit components, with the constraints that the cell capacitance, chosen as 15pF, and membrane resistance, chosen as 1GΩ, are in the range of the observed data (as is, consequently, its time constant which is 15ms with these choices); see Table 1 of the manuscript. We chose the capacitance of the soma as 1.5pF, making the time constant of the soma (1.5ms) an order of magnitude shorter than that of the cell.
Figure 1: Simplified circuit of a small soma (left parallel RC circuit) and the much larger remainder of a cell (right parallel RC circuit) connected by a neurite (right 100MΩ resistor). A current source (far left) injects constant current into the soma through the left 100MΩ resistor.
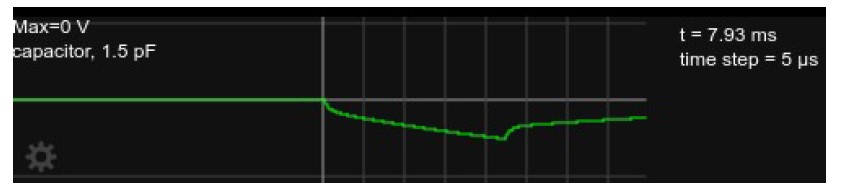
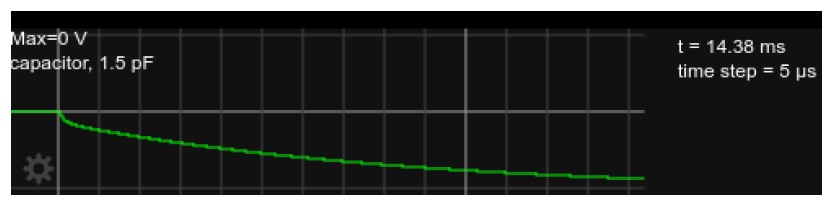
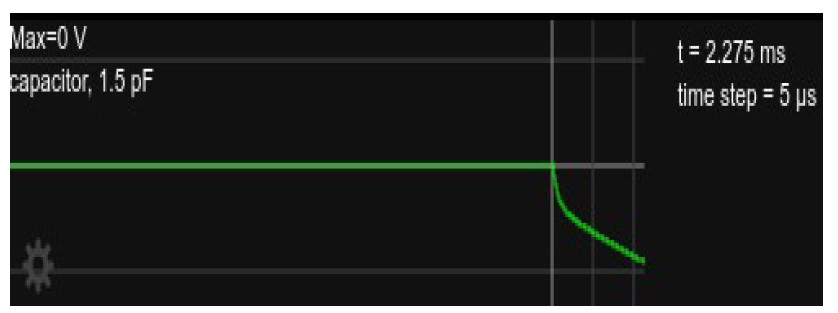
Figure 2 shows the somatic voltage in this circuit (i.e., at the upper terminal of the 1.5pF capacitor) while a -10pA current is injected for about 4.5ms, after which the current is set back to zero. The combination of initial rapid change, followed by a gradual change with a time constant of ≈ 15ms is visible at both onset and offset of the current injection. Figure 3 show the voltage traces plotted for a duration of approximately one time constant, and Fig 4 shows the detailed shape right after current onset.
Figure 2: Somatic voltage in the circuit in Fig. 1 with current injection for about 4.5ms, followed by zero current injection for another ≈ 3.5ms.
Figure 3: Somatic voltage in the circuit, as in Fig. 2 but with current injected for approx. 15msvvvvv
While we did not try to quantitatively assess the deviation from a single-exponential shape of the voltage in Fig. 2E, a more rapid increase at the onset and offset of the current injection is clearly visible in this Figure. This deviation from a single exponential is smaller than what we see in the simulation (both in Fig 2D of the manuscript, and in the results of the simplified circuit here in the rebuttal). We believe that the effect is smaller in Fig. E because it shows the average over many traces. It is much more visible in the ’raw’ (not averaged) traces. Two randomly selected traces from the first of the recorded neurons are shown in Figure 2 Supplement 2 C. While the non-averaged traces are plagued by artifacts and noise, the rapid voltage changes are visible essentially at all onsets and offsets of the current injection.
Figure 4: Somatic voltage in the circuit, as in Fig. 2 but showing only for the time right after current onset, about 2.3ms.
We have added a short discussion of this at the end of Section 2.3 to briefly point out this observation and its explanation. We there also refer to the simplified circuit simulation and comparison with raw voltage traces which is now shown in the new Figure 2 Supplement 2.
- The time constant in Table 1 is much shorter than in Figure 1FG?
No, these values are in agreement. To facilitate the comparison we now include a graphical measurement of tau from our traces in Figure 1 Supplement 2 J.
- Related to this, the capacitance values are very low maybe this can be explained by the model’s wrong assumption of tau?
Indeed, the measured time constants are somewhat lower than what might be expected. We believe that this is because after a step change of the injected current, an initial rapid voltage change occurs in the soma, where the recordings are taken. The measured time constant is a combination of the ’actual’ time constant of the cell and the ’somatic’ (very short) time constant of the soma. Please see our explanations above.
Importantly, the value for tau from Table 1 is not used explicitly in the model as the parameters used in our simulation are determined by optimal fits of the simulated voltage curves to experimentally obtained data.
- That latter in turn could be because of either space clamp issues in this hugely complex cell or bad model predictions due to incomplete reconstructions, bad match between morphology and electrophysiology (both are from different datasets?), or unknown ion channels that produce non-linear behaviour during the current injections.
Please see our detailed discussion above. Furthermore, we now provide additional recordings using cytoplasmic GFP as a marker for the identification of MBON-alpha3 and confirm our findings. We agree that space-clamp issues could interfere with our recordings in such a complex cell. However, our approach using electrophysiological data should still be superior to any other approach (picking text book values). As we injected negative currents for our analysis at least voltage-gated ion channels should not influence our recordings.
- The PRAXIS method in NEURON seems too ad hoc. Passive properties of a neuron should probably rather be explored in parameter scans.
We are a bit at a loss of what is meant by the PRAXIS method being "too ad hoc." The PRAXIS method is essentially a conjugate gradient optimization algorithm (since no explicit derivatives are available, it makes the assumption that the objective function is quadratic). This seems to us a systematic way of doing a parameter scan, and the procedure has been used in other related models, e.g. the cited Gouwens & Wilson (2009) study.
Questions I have:
- Computational aspects were previously addressed by e.g. Larry Abbott and Gilles Laurent (sparse coding), how do the findings here distinguish themselves from this work
In contrast to the work by Abbott and Laurent that addressed the principal relevance and suitability of sparse and random coding for the encoding of sensory information in decision making, here we address the cellular and computational mechanisms that an individual node (KC>MBON) play within the circuitry. As we use functional and morphological relevant data this study builds upon the prior work but significantly extends the general models to a specific case. We think this is essential for the further exploration of the topic.
- What is valence information?
Valence information is the information whether a stimulus is good (positive valence, e.g. sugar in appetitive memory paradigms, or negative valence in aversive olfactory conditioning - the electric shock). Valence information is provided by the dopaminergic system. Dopaminergic neurons are in direct contact with the KC>MBON circuitry and modify its synaptic connectivity when olfactory information is paired with a positive or negative stimulus.
- It seems that Martin Nawrot’s work would be relevant to this work
We are aware of the work by the Nawrot group that provided important insights into the processing of information within the olfactory mushroom body circuitry. We now highlight some of his work. His recent work will certainly be relevant for our future studies when we try to extend our work from an individual cell to networks.
- Compactification and democratization could be related to other work like Otopalik et al 2017 eLife but also passive normalization. The equal efficiency in line 427 reminds me of dendritic/synaptic democracy and dendritic constancy
Many thanks for pointing this out. This is in line with the comments from reviewer 1 and we now highlight these papers in the relevant paragraph in the discussion (line 442ff).
- The morphology does not obviously seem compact, how unusual would it be that such a complex dendrite is so compact?
We should have been more careful in our terminology, making clear that when we write ’compact’ we always mean ’electrotonically compact," in the sense that the physical dimensions of the neuron are small compared to its characteristic electrotonic length (usually called λ). The degree of a dendritic structure being electrotonically compact is determined by the interaction of morphology, size and conductances (across the membrane and along the neurites). We don’t believe that one of these factors alone (e.g. morphology) is sufficient to characterize the electrical properties of a dendritic tree. We have now clarified this in the relevant section.
- What were the advantages of using the EM circuit?
The purpose of our study is to provide a "realistic" model of a KC>MBON node within the memory circuitry. We started our simulations with random synaptic locations but wondered whether such a stochastic model is correct, or whether taking into account the detailed locations and numbers of synaptic connections of individual KCs would make a difference to the computation. Therefore we repeated the simulations using the EM data. We now address the point between random vs realistic synaptic connectivity in Figure 4F. We do not observe a significant difference but this may become more relevant in future studies if we compute the interplay between MBONs activated by overlapping sets of KCs. We simply think that utilizing the EM data gets us one step closer to realistic models.
- Isn’t Fig 4E rather trivial if the cell is compact?
We believe this figure is a visually striking illustration that shows how electrotonically compact the cell is. Such a finding may be trivial in retrospect, once the data is visualized, but we believe it provides a very intuitive description of the cell behavior.
Overall, I am worried that the passive modelling study of the MBON-a3 does not provide enough evidence to explain the electrophysiological behaviour of the cell and to make accurate predictions of the cell’s responses to a variety of stochastic KC inputs.
In our view our model adequately describes the behavior of the MBON with the most minimal (passive) model. Our approach tries to make the least assumptions about the electrophysiological properties of the cell. We think that based on the current knowledge our approach is the best possible approach as thus far no active components within the dendritic or axonal compartments of Drosophila MBONs have been described. As such, our model describes the current status which explains the behavior of the cell very well. We aim to refine this model in the future if experimental evidence requires such adaptations.
Reviewer #3 (Public Review):
This manuscript presents an analysis of the cellular integration properties of a specific mushroom body output neuron, MBON-α3, using a combination of patch clamp recordings and data from electron microscopy. The study demonstrates that the neuron is electrotonically compact permitting linear integration of synaptic input from Kenyon cells that represent odor identity.
Strengths of the manuscript:
The study integrates morphological data about MBON-α3 along with parameters derived from electrophysiological measurements to build a detailed model. 2) The modeling provides support for existing models of how olfactory memory is related to integration at the MBON.
Weaknesses of the manuscript:
The study does not provide experimental validation of the results of the computational model.
The goal of our study is to use computational approaches to provide insights into the computation of the MBON as part of the olfactory memory circuitry. Our data is in agreement with the current model of the circuitry. Our study therefore forms the basis for future experimental studies; those would however go beyond the scope of the current work.
The conclusion of the modeling analysis is that the neuron integrates synaptic inputs almost completely linearly. All the subsequent analyses are straightforward consequences of this result.
We do, indeed, find that synaptic integration in this neuron is almost completely linear. We demonstrate that this result holds in a variety of different ways. All analyses in the study serve this purpose. These results are in line with the findings by Hige and Turner (2013) who demonstrated that also synaptic integration at PN>KC synapses is highly linear. As such our data points to a feature conservation to the next node of this circuit.
The manuscript does not provide much explanation or intuition as to why this linear conclusion holds.
We respectfully disagree. We demonstrate that this linear integration is a combination of the size of the cell and the combination of its biophysical parameters, mainly the conductances across and along the neurites. As to why it holds, our main argument is that results based on the linear model agree with all known (to us) empirical results, and this is the simplest model.
In general, there is a clear takeaway here, which is that the dendritic tree of MBON-α3 in the lobes is highly electrotonically compact. The authors did not provide much explanation as to why this is, and the paper would benefit from a clearer conclusion. Furthermore, I found the results of Figures 4 and 5 rather straightforward given this previous observation. I am sceptical about whether the tiny variations in, e.g. Figs. 3I and 5F-H, are meaningful biologically.
Please see the comment above as to the ’why’ we believe the neuron is electrotonically compact: a model with this assumption agrees well with empirically found results.
We agree that the small variations in Fig 5F-H are likely not biologically meaningful. We state this now more clearly in the figure legends and in the text. This result is important to show, however. It is precisely because these variations are small, compared to the differences between voltage differences between different numbers of activated KCs (Fig 5D) or different levels of activated synapses (Fig 5E) that we can conclude that a 25% change in either synaptic strength or number can represent clearly distinguishable internal states, and that both changes have the same effect. It is important to show these data, to allow the reader to compare the differences that DO matter (Fig 5D,E) and those that DON’T (Fig 5F-H).
The same applies to Fig 3I. The reviewer is entirely correct: the differences in the somatic voltage shown in Figure 3I are minuscule, less than a micro-Volt, and it is very unlikely that these difference have any biological meaning. The point of this figure is exactly to show this!. It is to demonstrate quantitatively the transformation of the large differences between voltages in the dendritic tree and the nearly complete uniform voltage at the soma. We feel that this shows very clearly the extreme "democratization" of the synaptic input!
-

eLife assessment
Detailed electron-microscopy reconstructions of neurons, which are now available for a complete Drosophila central brain, raise the prospect of detailed models of their electrical properties. This manuscript uses a recently released dataset to model one particular neuron in an olfactory learning center of the fly brain. The model elucidates how this neuron responds to synaptic inputs that represent odor, suggesting how modification of these synapses might underlie olfactory memory. This work brings together electrophysiological recordings and neuroanatomical reconstructions from volume electron microscopy to model how a neuronal arbor integrates synaptic inputs. With the many ongoing connectome mapping projects world wide, the results here can illustrate an approach to interpretation of connectomes towards understanding …
eLife assessment
Detailed electron-microscopy reconstructions of neurons, which are now available for a complete Drosophila central brain, raise the prospect of detailed models of their electrical properties. This manuscript uses a recently released dataset to model one particular neuron in an olfactory learning center of the fly brain. The model elucidates how this neuron responds to synaptic inputs that represent odor, suggesting how modification of these synapses might underlie olfactory memory. This work brings together electrophysiological recordings and neuroanatomical reconstructions from volume electron microscopy to model how a neuronal arbor integrates synaptic inputs. With the many ongoing connectome mapping projects world wide, the results here can illustrate an approach to interpretation of connectomes towards understanding neural circuit function. The rules of synaptic plasticity discussed here furthermore do not only shed light into the mechanisms of learning and memory in biological systems but also inspire the formulation of new approaches to adjusting connection weights in artificial neural networks.
-

Reviewer #1 (Public Review):
Hafez and collaborators describe the construction and analysis of a computational model of a mushroom body neuron. The anatomy derives from a combination of electron microscopy reconstructions of MBON-α3 and also from light microscopy. The physiological parameters derive from publications that measured them, in addition to the author's own electrophysiological recordings with patch-clamp.
There are two main findings. First, the dendritic arbor of MBON-α3 is electrotonically compact, meaning, individual connections from Kenyon cells will similarly elicit action potentials independently as to where, spatially, the synapses lay on the arbor. Second, in simulation, exploration of changes in the strength of Kenyon cell inputs illustrate two possible ways to alter the strength of the KC-MBON physiological …
Reviewer #1 (Public Review):
Hafez and collaborators describe the construction and analysis of a computational model of a mushroom body neuron. The anatomy derives from a combination of electron microscopy reconstructions of MBON-α3 and also from light microscopy. The physiological parameters derive from publications that measured them, in addition to the author's own electrophysiological recordings with patch-clamp.
There are two main findings. First, the dendritic arbor of MBON-α3 is electrotonically compact, meaning, individual connections from Kenyon cells will similarly elicit action potentials independently as to where, spatially, the synapses lay on the arbor. Second, in simulation, exploration of changes in the strength of Kenyon cell inputs illustrate two possible ways to alter the strength of the KC-MBON physiological connection, showing that either could account for the observed synaptic depression in the establishment of associative memories. The properties of each approach differ.
Overall, the manuscript clearly describes the journey from connectomics and electrophysiology to computational modeling and exploration of the physiological properties of a circuit in simulation.
-

Reviewer #2 (Public Review):
"The cellular architecture of memory modules in Drosophila supports stochastic input integration" is a classical biophysical compartmental modelling study. It takes advantage of some simple current injection protocols in a massively complex mushroom body neuron called MBON-a3 and compartmental models that simulate the electrophysiological behaviour given a detailed description of the anatomical extent of its neurites.
This work is interesting in a number of ways:
- The input structure information comes from EM data (Kenyon cells) although this is not discussed much in the paper
- The paper predicts a potentially novel normalization of the throughput of KC inputs at the level of the proximal dendrite and soma
- It claims a new computational principle in dendrites, this didn't become very clear to meProblems …
Reviewer #2 (Public Review):
"The cellular architecture of memory modules in Drosophila supports stochastic input integration" is a classical biophysical compartmental modelling study. It takes advantage of some simple current injection protocols in a massively complex mushroom body neuron called MBON-a3 and compartmental models that simulate the electrophysiological behaviour given a detailed description of the anatomical extent of its neurites.
This work is interesting in a number of ways:
- The input structure information comes from EM data (Kenyon cells) although this is not discussed much in the paper
- The paper predicts a potentially novel normalization of the throughput of KC inputs at the level of the proximal dendrite and soma
- It claims a new computational principle in dendrites, this didn't become very clear to meProblems I see:
- The current injections did not last long enough to reach steady state (e.g. Figure 1FG), and the model current injection traces have two time constants but the data only one (Figure 2DF). This does not make me very confident in the results and conclusions.
- The time constant in Table 1 is much shorter than in Figure 1FG?
- Related to this, the capacitance values are very low maybe this can be explained by the model's wrong assumption of tau?
- That latter in turn could be because of either space clamp issues in this hugely complex cell or bad model predictions due to incomplete reconstructions, bad match between morphology and electrophysiology (both are from different datasets?), or unknown ion channels that produce non-linear behaviour during the current injections.
- The PRAXIS method in NEURON seems too ad hoc. Passive properties of a neuron should probably rather be explored in parameter scans.Questions I have:
- Computational aspects were previously addressed by e.g. Larry Abbott and Gilles Laurent (sparse coding), how do the findings here distinguish themselves from this work
- What is valence information?
- It seems that Martin Nawrot's work would be relevant to this work
- Compactification and democratization could be related to other work like Otopalik et al 2017 eLife but also passive normalization. The equal efficiency in line 427 reminds me of dendritic/synaptic democracy and dendritic constancy
- The morphology does not obviously seem compact, how unusual would it be that such a complex dendrite is so compact?
- What were the advantages of using the EM circuit?
- Isn't Fig 4E rather trivial if the cell is compact?Overall, I am worried that the passive modelling study of the MBON-a3 does not provide enough evidence to explain the electrophysiological behaviour of the cell and to make accurate predictions of the cell's responses to a variety of stochastic KC inputs.
-

Reviewer #3 (Public Review):
This manuscript presents an analysis of the cellular integration properties of a specific mushroom body output neuron, MBON-α3, using a combination of patch clamp recordings and data from electron microscopy. The study demonstrates that the neuron is electrotonically compact permitting linear integration of synaptic input from Kenyon cells that represent odor identity.
Strengths of the manuscript:
- The study integrates morphological data about MBON-α3 along with parameters derived from electrophysiological measurements to build a detailed model.
- The modeling provides support for existing models of how olfactory memory is related to integration at the MBON.
Weaknesses of the manuscript:
- The study does not provide experimental validation of the results of the computational model.
- The conclusion of the modeling …
Reviewer #3 (Public Review):
This manuscript presents an analysis of the cellular integration properties of a specific mushroom body output neuron, MBON-α3, using a combination of patch clamp recordings and data from electron microscopy. The study demonstrates that the neuron is electrotonically compact permitting linear integration of synaptic input from Kenyon cells that represent odor identity.
Strengths of the manuscript:
- The study integrates morphological data about MBON-α3 along with parameters derived from electrophysiological measurements to build a detailed model.
- The modeling provides support for existing models of how olfactory memory is related to integration at the MBON.
Weaknesses of the manuscript:
- The study does not provide experimental validation of the results of the computational model.
- The conclusion of the modeling analysis is that the neuron integrates synaptic inputs almost completely linearly. All the subsequent analyses are straightforward consequences of this result.
- The manuscript does not provide much explanation or intuition as to why this linear conclusion holds.
In general, there is a clear takeaway here, which is that the dendritic tree of MBON-α3 in the lobes is highly electrotonically compact. The authors did not provide much explanation as to why this is, and the paper would benefit from a clearer conclusion. Furthermore, I found the results of Figures 4 and 5 rather straightforward given this previous observation. I am sceptical about whether the tiny variations in, e.g. Figs. 3I and 5F-H, are meaningful biologically.
-